Fraleigh 현대대수학 2 탐구 노트

개요

10월 한 달 동안 현대대수학 2의 내용에 해당하는 내용들을 공부했다. 저번 현대대수학 1과 마찬가지로 공부한 내용들을 간단하게 정리해보려고 한다.

참고로 공부 방식은 개념 이해 및 “Theory”에 해당하는 연습 문제를 모두 푸는 것으로 진행했으며, 공부 방법에 대한 자세한 설명을 글의 마지막에 적어놓았다.

이번 글에서 다루는 주제는 다음과 같다.

Chapter 34: 그림으로 이해하는 Isomorphism Theorems
Chapter 37: Sylow Theorem의 활용법
Chapter 48~53: Galois Theory에서 splitting field와 separable extension의 역할
Chapter 56: extensions by radicals(거듭제곱근 확대) 분석 방법 정리

공부 기간: 10/10 ~ 11/3 (3.5주)

현대대수학 2 파트의 특징

시작에 앞서, 현대대수학 2 파트의 특징에 대해서 간단한 생각을 말하고자 한다.
이 부분의 내용들은 기본적으로 그 전에 배웠던 개념들을 응용하는 식으로 이루어진다.

[VII] Advanced Group Theory: normal group에 대한 이해 필요
[IX] Factorization: ideal에 대한 이해 필요
[X] Automorphisms and Galois theory: $\overline{F}$ (algebraic closure)에 대한 이해, solvable group (더 포괄적으로 series of groups)에 대한 이해 필요

이런 식으로 이전에 다왔던 개념에 조금씩 내용을 더붙여가는 식으로 진행된다. 따라서 현대대수학 1 파트에 대한 이해가 부족하면 도저히 읽을수가 없는 수준이기에, 이전 개념에 대한 확실한 이해가 더욱 중요한 파트라고 할 수 있겠다.

나 또한 algebraic closure에 대해 정확히 이해하지 못한 상태에서 [X] Automorphisms and Galois theory 를 공부하다가 고생을 좀 했는데, 현대대수학 2를 공부할 예정이라면 앞 부분 내용을 잘 이해하고 있는 것을 추천한다.

그림으로 이해하는 Isomorphism Theorems

첫 번째 주제는 Isomorphism Theorem(동형 정리)이다. 현대대수학 2 공부를 시작하고 처음으로 마주한 챕터이면서 중요도 또한 매우 높다고 할 수 있다. 그 다음 챕터인 Series of Groups부터 본격적으로 군을 서로 곱하고 나누고 하면서 험하게 다루기 시작하는데, 그 과정에서 이 동형 정리가 밥먹듯이 사용되기 때문이다.

그럼에도 불구하고 해당 정리가 의미하는 내용이 머릿속에 쉽게 그려질 때 까지는 꽤 시간이 걸렸다. 나와 같은 사람들을 위해서 동형 정리를 그림으로 깔끔하게 정리해 보았다. 증명과 함께 그림을 보면 이해가 쉬울 것이라고 생각한다.

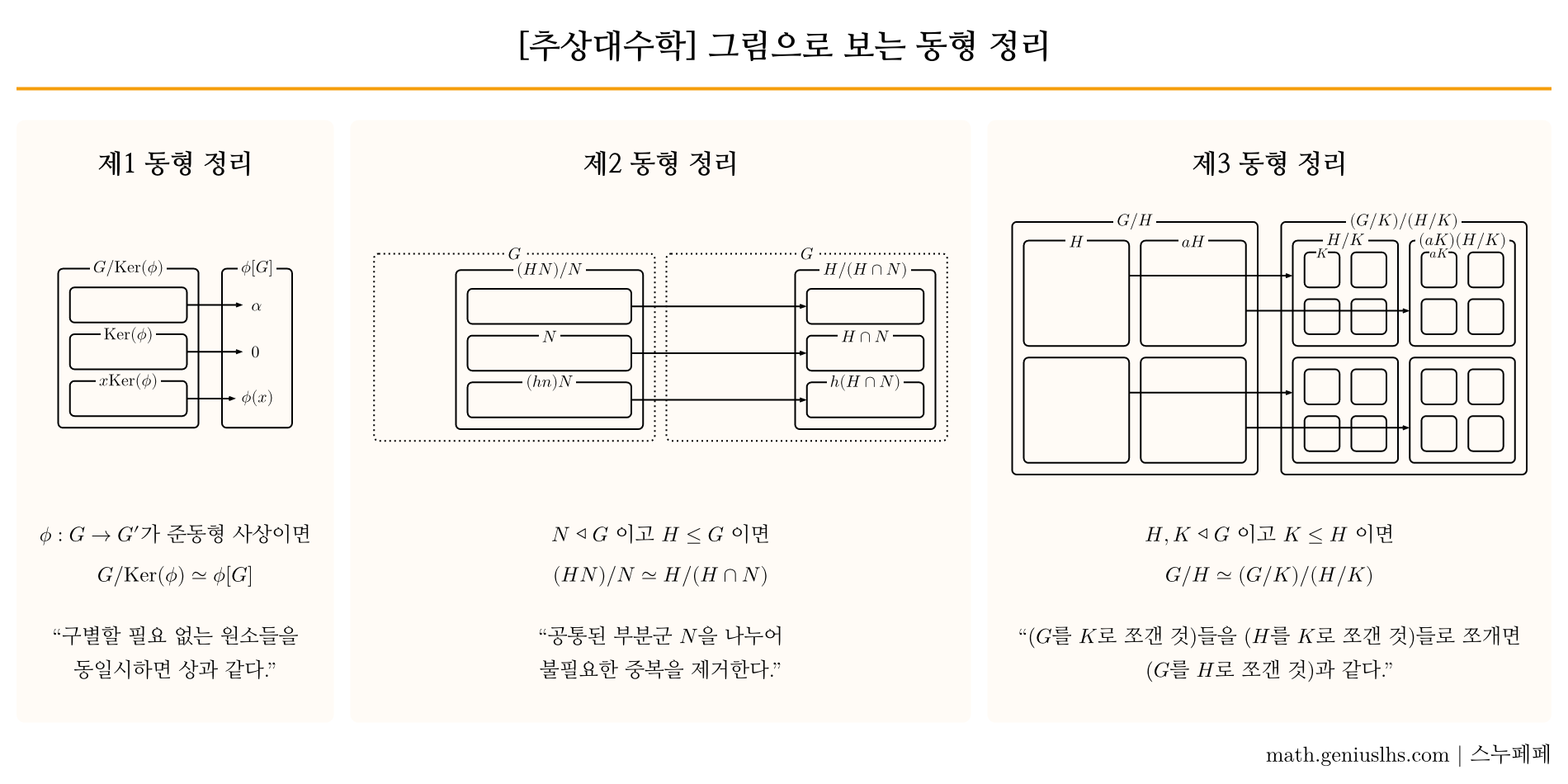그림으로 보는 동형 정리

Theorem 34.2 (제1 동형 정리)

$\phi: G \to G'$가 준동형 사상이면 $G/\text{Ker}(\phi) \simeq \phi[G]$ 이다. 나아가 유일한 동형 사상 $\mu: G/\text{Ker}(\phi) \to \phi[G]$가 존재하여 $\phi(x) = \mu(\gamma_K(x))$를 만족한다. ($\gamma_K: G \to G/K$는 canonical homomorphism이다.)

증명. 생략.

해당 내용과 관련해서 이전 글(현대대수학 1 탐구노트)에서는 몫군이 어떤 배경에서 등장하였는지 다룬적이 있다.

Theorem 34.5 (제2 동형 정리)

$H$가 $G$의 부분군이고 $K$가 $G$의 정규부분군이면 $(HN)/N \simeq H/(H \cap N)$ 이다.

증명. $\gamma: G \to G/N$이 canonical homomorphism이라고 하자. $H \le G$ 이므로 $\gamma[H]$는 $\gamma[G] = G/N$의 부분군이다. 이제 $\gamma$의 정의역을 $H$로 제한한 준동형 사상 $\gamma_H: H \to \gamma[H]$를 고려하자. 이 사상의 kernel은 $N$에 속하면서도 $H$에 속하는 원소들, 즉 $H \cup N$이다. 따라서 제1 동형 정리에 의해 동형 사상 $\mu_1: H/(H \cap N) \to \gamma[H]$가 존재한다.

한편 $\gamma_{HN}: HN \to \gamma[H]$ 또한 전사인 준동형 사상인데, 모든 $n \in N$에 대하여 $\gamma(n)$은 $G/N$의 항등원인 $N$이기 때문이다. 또한 이 사상의 kernel은 $N$이므로 제1 동형 정리에 의해 동형 사상 $\mu_2: (HN)/N \to \gamma[H]$가 존재한다.

이 둘을 종합하면 $\phi = \mu_1^{-1} \mu_2$은 우리가 원하던 동형 사상이다. 그림에서 볼 수 있듯이 대응관계는 다음과 같음을 알 수 있다.

$$\phi((hn)N) = h(H \cap N)$$

Theorem 34.7 (제3 동형 정리)

$H$와 $K$가 $G$의 정규부분군이고 $K \le H$이면 $G/H \simeq (G/K)/(H/K)$ 이다.

증명. $\phi: G \to (G/K)/(H/K)$를 $\phi (a) = (aK)(H/K)$와 같이 정의하자. 자명하게 $\phi$는 전사함수이다. 또한 임의의 $a, b \in G$에 대하여

$$\begin{equation*} \begin{split} \phi(ab) &= [(ab)K](H/K) = [(aK)(bK)](H/K) \\ &= [(aK)(H/K)][(bK)(H/K)] \\ &= \phi(a)\phi(b) \end{split} \end{equation*}$$

이므로 $\phi$는 준동형사상이다. 한편 $\phi$의 kernel은 $\phi(x)=H/K$를 만족하는 $x \in G$들로 이루어져 있는데, 이는 정확히 $H$의 원소들과 같다. 따라서 제1 동형 정리에 의해 $G/H /simeq (G/K)/(H/K)$ 이다.

Sylow Theorem의 활용법

Sylow Theorem은 유한군의 구조를 분석할 수 있는 유용한 도구이다. 이번 글에서는 Sylow Theorem의 자세한 증명은 생략하고, 실제로 유한군의 분석에 어떻게 응용될 수 있는지를 살펴보고자 한다. 조금 더 자세하게 말하자면, 아래 그림의 우측 상단에 있는 위수에 따른 성질 중에서 $|G|=pq$인 경우와 $|G|=p^2$인 경우를 증명할 것이다.

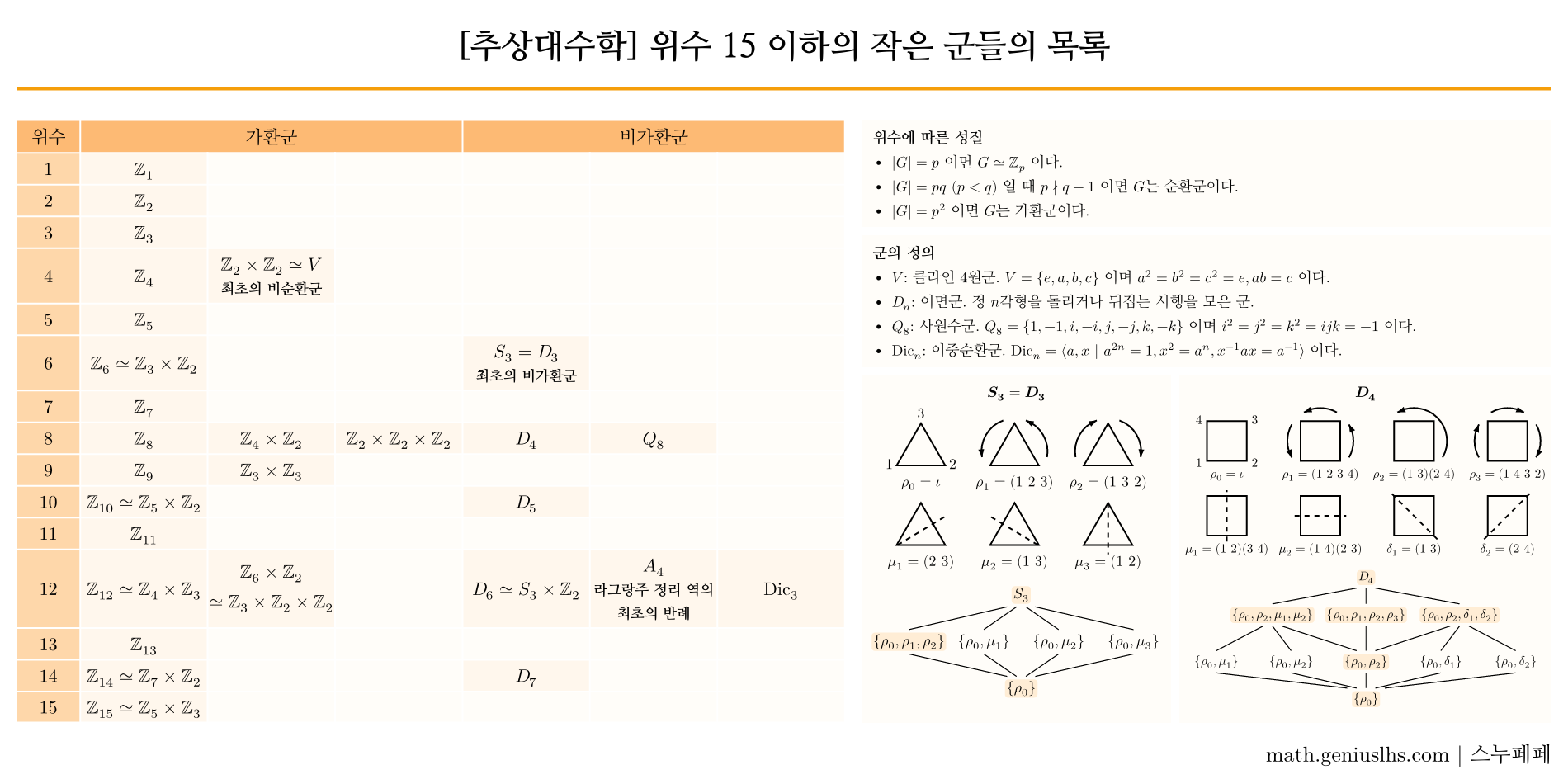위수 15 이하의 작은 군들의 목록

참고로 위 그림은 위수에 따른 유한군들의 목록을 정리한 것인데, 위 목록을 눈에 익혀 놓으면 꽤 도움이 된다.
왜냐하면 Free Group 단원에서 군의 위수와 특성(abelian 등)만을 가지고 어떤 군과 동형인지 파악하는 내용이 나오고, 학교 시험에서도 특정 군의 구조를 분석하는 문제가 출제되기도 하기 때문이다.
이를테면 찾고자 하는 군의 위수가 6임을 알았을 때, 가능한 군이 $\Z_6$과 $S_3$ 뿐임을 알고 있다면 주어진 군이 가환군인지 판별하면 되겠구나 하는 계획을 세울 수 있다.

우선 실로우 정리를 간단하게 언급하겠다.

Theorem 36.8 (First Sylow Theorem)
Let $G$ be a finite group and let $|G|=p^n m$ where $n \ge 1$ and where $p$ does not divide $m$. Then

1. $G$ contains a subgroup of order $p^i$ for each $i$ where $1 \le i \le n$,
2. Every subgroup $H$ of $G$ of order $p^i$ is a normal subgroup of a subgroup of order $p^{i+1}$ for $1 \le i < n$.

Theorem 36.10 (Second Sylow Theorem)
Let $P_1$ and $P_2$ be Sylow $p$-subgroups of a finite group $G$. Then $P_1$ and $P_2$ are conjugate subgroups of $G$.

Theorem 36.11 (Third Sylow Theorem)
If $G$ is a finite group and $p$ divides $|G|$, then the number of Sylow $p$-subgroups is congruent to $1$ modulo $p$ and divides $|G|$.

위 성질을 증명하기 위해서는 추가적으로 2개의 도구가 더 필요하다.

Exercise 36.12
Let $G$ be a finite group and let primes $p$ and $q \neq p$ divide $|G|$. Prove that if $G$ has precisely one proper Sylow $p$-subgroup, it is a normal subgroup, so $G$ is not simple.

증명. $G$의 Sylow $p$-subgroup을 $H$라고 하자. 그러면 $q$가 $|G|$의 약수이므로 $H \neq G$이다. 이제 임의의 $g \in G$에 대해 $g H g^{-1}$도 Sylow $p$-subgroup인데, $G$는 유일한 Sylow $p$-subgroup을 가지므로 $g H g^{-1} = H$이다. 따라서 $H$는 $G$의 proper 정규부분군이고, $G$는 simple group이 아니다.

Lemma 37.5
Let $G$ be a group containing normal subgroups $H$ and $K$ such that $H \cap K = {e}$ and $H \vee K=G$. Then $G$ is isomorphic to $H \times K$.

참고. $H \vee K$는 $HK=\{hk | h \in H, k \in K\}$를 포함하는 가장 작은 군이다.
증명. 우선 모든 $k \in K$와 $h \in H$에 대해 $hk=kh$임을 보인다. $hkh^{-1}k^{-1}=(hkh^{-1})k^{-1}=h(kh^{-1}k^{-1})$를 고려하자. $H$와 $K$가 $G$의 정규부분군이므로, $hkh^{-1}k^{-1}$은 $H$와 $K$에 동시에 속한다. $K \cap H =\{e\}$이므로 $hkh^{-1}k^{-1}=e$이며, 따라서 $hk=kh$이다.
이제 $\phi: H \times K \to G$를 $\phi(h,k)=hk$와 같이 정의하자. 그러면

$$\phi((h,k)(h',k'))=\phi(hh',kk')=hh'kk'=h k h' k' = \phi(h,k) \phi(h',k')$$

이므로 $\phi$는 준동형사상이다.
만약 $\phi(h,k)=e$이면 $hk=e$이고 $h=k^{-1}$이다. 좌변과 우변 모두 $H \cup K$에 속하므로 $h=k=e$이고, 따라서 $\text{Ker}(\phi)=\{(e,e)\}$이므로 $\phi$는 one-to-one이다.
또한 $H$와 $K$가 정규부분군이므로 $HK=H \vee K$이고, 가정에 의해 $H \vee K = G$이다. 따라서 $\phi$는 전사이고 $H \times K \simeq G$를 얻는다.

이제 본 명제의 증명은 다음과 같다.

Theorem 37.6
For a pime number $p$, every group $G$ of order $p^2$ is abelian.

증명. 만약 $G$가 순환군이 아니라면 $e$를 제외한 모든 원소의 위수는 $p$여야 한다. 그러한 원소들 중 하나를 $a$라고 하자. 순환부분군 $\lang a \rang$은 $G$를 전부 채우지 못하므로, $b \notin \lang a \rang$인 $b \in G$를 하나 더 고를 수 있다. 또한 $\lang a \rang \cap \lang b \rang = \{e\}$인데, 만약 $c \neq e$인 원소 $c \in \lang a \rang \cap \lang b \rang$가 존재한다면 $c$가 $\lang a \rang$와 $\lang b \rang$를 둘다 생성하므로 $\lang a \rang = \lang b \rang$가 되어 모순이기 때문이다.
이제 First Sylow Theorem에 의해 $\lang a \rang$는 [위수가 $p^2$인 어떤 $G$의 부분군]의 정규부분군이다. 즉, $G$의 정규부분군이다. 마찬가지로 $\lang b \rang$ 또한 $G$의 정규부분군이다. 이제 $\lang a \rang \vee \lang b \rang$는 $\lang a \rang$를 properly 포함하고 위수가 $p^2$의 약수인 $G$의 부분군인데, 이는 정확히 $G$와 같다. 따라서 Lemma 37.5에 의해 $G$는 $\lang a \rang \times \lang b \rang$와 동형이고, 따라서 가환이다.

Theorem 37.7
If $p$ and $q$ are distinct primes with $p<q$, then every group $G$ of order $pq$ has a single subgroup of order $q$ and this subgroup is normal in $G$. Hence $G$ is not simple. If $q$ is not congruent to $1$ modulo $p$, then $G$ is abelian and cyclic.

증명. First Sylow Theorem과 Third Sylow Theorem에 의해 $G$는 Sylow $q$-subgroup을 가지고, 그 개수는 modulo $q$로 $1$과 같으며 $pq$의 약수이다. $p<q$이므로 이를 만족하는 수는 $1$ 밖에 없다. 따라서 정확히 한 개의 $q$-subgroup $Q$가 존재한다. Exercise 36.12에 의해 $Q$는 $G$의 정규부분군이고, $G$는 단순군이 아니다.
비슷하게, $G$는 Sylow $p$-subgroup $P$를 가지며 그 개수는 modulo $p$로 $1$과 같고 $pq$의 약수이다. 만약 $q \not \equiv 1 (\text{mod} \, p)$이라면 개수는 정확히 한 개이고, $P$는 $G$의 정규부분군이다. $e$를 제외한 $Q$의 모든 원소의 위수는 $q$이고, $e$를 제외한 $P$의 모든 원소의 위수는 $p$이므로 $Q \cap P = \{e\}$이다. 또한 $Q \vee P$는 $Q$를 properly 포함하고 위수가 $pq$의 약수이므로 $G$와 같을 수 밖에 없다. 따라서 Lemma 37.5에 의해 $G$는 $Q \times P$, 즉 $\Z_q \times \Z_p$와 동형이다. 따라서 $G$는 가환군이면서 순환군이다.

Galois Theory에서 splitting field와 separable extension의 역할

Galois Theory에서 splitting field와 separable extension의 역할이 무엇인지를 간단하게 생각해보았다.

우선 해당 개념들이 등장한 배경은 다음과 같다. 우리는 갈루아 군 $G(E/F)$의 원소의 개수를 계산하고자 한다. 왜냐하면 어떤 군을 분석할 때 그 군의 위수는 가장 기본적인 분석 대상이면서, 많은 정보를 가져다주기 때문이다. 그런데 가만히 생각해보면, $|G(E/F)|$는 $[E:F]$와 밀접한 연관이 있는 것 같다.

이를테면 가장 간단한 simple extension의 경우를 살펴보자. primitive $n$th root of unity in $\Complex$ (즉, $\zeta^n=1$를 만족하는) $\zeta \in \overline{F}$에 대해 $E=F(\zeta)$를 생각하자. 각각의 $\sigma \in G(E/F)$는 $\sigma(\zeta)$에 의해 결정되는데, $\sigma(\zeta)$는 $\zeta^0, \zeta^1, \cdots, \zeta^{n-1}$중 하나일 수 밖에 없으므로 $|G(E/F)|=n$ 이다. 따라서 이 경우에 $|G(E/F)| = [E:F]$이 성립함을 볼 수 있다. 이외에도 $|G(\mathbf{Q} (\sqrt{2},\sqrt{3})/\\mathbf{Q})|=4=[\mathbf{Q}(\sqrt{2},\sqrt{3}), \mathbf{Q}]$와 같은 예시는 이 관계가 우연이 아님을 시사한다.

우리는 $|G(E/F)| = [E:F]$를 증명하기 위해, 하나의 징검다리 $\{E:F\}$를 도입한다.

Definition 49.9
Let $E$ be a finite extension of a field $F$. The number of isomorphisms of $E$ onto a subfield of $\overline{F}$ leaving $F$ fixed is the index $\{E:F\}$ of $E$ over $F$.

이후에 논의하겠지만 세 개의 값 사이에는 다음과 같은 부등식이 성립한다.

$$|G(E/F)| \le \{E:F\} \le [E:F]$$

그렇다면 등호가 성립하는 경우는 언제일까?

1. 우선 $|G(E/F)| = \{E:F\}$일 조건을 생각해보자. 여기서 우리는 $G(E/F)$와 $\{E:F\}$에서 고려하는 isomorphism의 차이를 알 필요가 있다. $G(E/F)$는 $E$에서 $E$로 가면서 $F$를 고정하는 isomorphism들(즉, automorphism이 된다)을 고려한다. 반면, $\{E:F\}$에서는 $E$에서 $\overline{F}$로 가면서 $F$를 고정하는 isomorphim $\sigma$를 고려한다. 그래서 이 경우에는 정의역 $E$에 속하는 원소가 $\sigma$에 의해 $E$ 밖으로 “샐 수” 있기 때문에 항상 $\sigma \in G(E/F)$라고 할 수 없는 것이고, 따라서 $\{E:F\}$보다 $|G(E/F)|$가 더 작거나 같은 것이다.

   그래서 $|G(E/F)| = \{E:F\}$이기 위해서는 $F$에서 $E$를 만들 때 아무 원소들이나 막 집어넣으면 안된다. 원소들이 $E$에서 $E$ 안으로만 향할 수 있도록 적당한 통제가 필요하며, 그 조건은 $F$를 계수로 하는 “특정 다항식들”이 존재하여 $E$가 해당 다항식들의 근을 포함하는 $F$의 가장 작은 확장체라는 것이다. 이는 책에서 제시하는 splitting field의 정의에서 볼 수 있다.

   Definition 50.1
   Let $F$ be a field with algebraic closure $\overline{F}$. Let $\{f_i (x) \, | \, i \in I\}$ be a collection of polynomials in $F[x]$. A field $E \le \overline{F}$ is the splitting field of $\{f_i (x) \, | \, i \in I\}$ over $F$ if $E$ is the smallest subfield of $\overline{F}$ containing $F$ and all the zeros in $\overline{F}$ of each of the $f_i (x)$ for $i \in I$. A field $K \le \overline{F}$ is a splitting field over $F$ if it is the splitting field of some set of polynomials in $F[x]$.

2. 다음으로 $\{E:F\} = [E:F]$일 조건을 생각해보자. 간단한 이해를 위해 simple extension $E=F(\alpha)$를 통해 살펴보자. 우리는 $\{E:F\}$가 $\text{irr}(\alpha,F)$와 밀접한 관계가 있음을 추측할 수 있다. 왜냐하면 $E$에서 $\overline{F}$로 가면서 $F$를 고정하는 임의의 isomorphism $\sigma$에 대해 $\sigma(\alpha)$는 $\text{irr}(\alpha,F) = 0$의 근 중 하나일 수밖에 없으므로, $\{E:F\}$는 $\text{irr}(\alpha,F) = 0$의 서로 다른 근의 개수와 같기 때문이다. 만약 $n=\text{deg}(\alpha,F)$차 다항식 $\text{irr}(\alpha,F)$가 $(x-2)^2(x-3)^2$와 같이 중근을 가진다면, $\{E:F\} = 2 \neq 4 = [E:F]$와 같이 등호가 성립하지 않을 것이다. 그래서, $\{E:F\} = [E:F]$이기 위해서는 반드시 $\text{irr}(\alpha,F)$가 중복도 1의 근들 만을 가져야 한다.

   page. 404 (Theorem 51.9 위)
   We know that $\{F(\alpha):F\}$ is the number of distinct zeros of $\text{irr}(\alpha,F)$. Also, the multiplicity of $\alpha$ in $\text{irr}(\alpha,F)$ is the same as the multiplicity of each conjugate of $\alpha$ over $F$, by Theorem 51.2. Thus $\alpha$ is separable over $F$ if and only if $\text{irr}(\alpha,F)$ has all zeros of multiplicity $1$. This tells us at once that an irreducible polynomial $f(x) \in F[x]$ is separable over $F$ if and only if $f(x)$ has all zeros of multiplicity $1$.

결론적으로, splitting field와 separable extension이라는 두 조건이 합쳐졌을 때 $|G(E/F)| = [E:F]$이 성립함을 알 수 있다. 그래서 우리는 이 두 조건을 합쳐 normal extension이라고 부른다.

Definition 53.1
A finite extension $K$ of $F$ is a finite normal extension of $F$ if $K$ is a separable splitting field over $F$.

extensions by radicals(거듭제곱근 확대) 분석 방법 정리

5차 방정식의 근의 공식이 없음을 증명하는 과정에서 등장하는 거듭제곱근 확대체를 분석하는 방법을 정리해보았다. 예전에 말했듯이 나는 $e^{x^2}$의 적분 불가능성에 큰 관심이 있는데, 해당 증명에서도 비슷한 흐름의 논리가 나올 것 같아 자세히 분석해 보았다.

Definition 56.1
An extension $K$ of a field $F$ is an extension of $F$ by radicals if there are elements $\alpha_1, \cdots, \alpha_r \in K$ and positive integers $n_1, \cdots n_r$ such that $K=F(\alpha_1, \cdots, \alpha_r)$, $\alpha_1^{n_1} \in F$ and $\alpha_i^{n_i} \in F(\alpha_1, \cdots,\alpha_{i-1})$ for $1<i \le r$. A polynomial $f(x) \in F[x]$ is solvable by radicals over $F$ if the splitting field $E$ of $f(x)$ over $F$ is contained in an extension of $F$ by radicals.

간단하게 말해서, 거듭제곱근 확대란 기존 체에 n제곱근들을 계속 가해서 만들 수 있는 확장체를 말한다.
이 개념은 실제로 5차 방정식의 근의 공식이 없음을 증명하는데 큰 역할을 한다. 만약 $\mathbf{Q}[x]$에 속하는 다항식에 대해 그 근이 extension by radicals에 포함되지 않는다면, 이는 곧 근의 공식이 없다는 것을 뜻하기 때문이다.

Lemma 56.3
Let $F$ be a field of characteristic $0$, and let $a \in F$. If $K$ is the splitting field of $x^n-a$ over $F$, then $G(K/F)$ is a solvable group.

증명. 생략.

우선 위와 같은 보조정리가 필요하다. 증명은 간단..하진 않지만 더 중요한 정리가 뒤에 나오므로 생략한다.

Theorem 56.4
Let $F$ be a field of characteristic zero, and let $F \le E \le K \le \overline{F}$, where $E$ is a normal extension of $F$ and $K$ is an extension of $F$ by radicals. Then $G(E/F)$ is a solvable group.

증명. 우선 $K$를 포함하고 [$F$의 finite normal extension by radicals]인 $L$이 존재하여 $G(L/F)$가 solvable이 됨을 보일 것이다. $K$가 extension by radicals이므로 정의에 의해 $K=F(\alpha_1, \cdots, \alpha_r)$이고 $\alpha_1^{n_1} \in F$, $\alpha_i^{n_i} \in F(\alpha_1, \cdots,\alpha_{i-1})$ for $1<i \le r$ 이다. 이제 $L$을 구성하기 위해서, 우선 $L_1$을 $f_1 (x) = x^{n_1}-\alpha_1^{n_1}$의 splitting field over $F$로 정의한다. 그러면 Lemma 56.3에 의해 $G(L_1/F)$은 solvable group이다.

이제 $\alpha_2^{n_2} \in L_1$ 임을 기억하며 다음과 같은 다항식을 생각한다.

$$f_2(x) = \displaystyle\prod_{\sigma \in G(L_1/F)} [x^{n_2} - \sigma(\alpha_2)^{n_2}]$$

이 다항식은 $G(L_1/F)$에 속하는 임의의 $\sigma$를 작용해도 변하지 않으므로 $f_2(x) \in F[x]$임을 알 수 있다. 이제 $L_2$를 $f_2(x)$의 splitting field over $L_1$으로 정의한다. 그러면 $L_2$는 splitting field over $F$이고, normal extension of $F$ by radicals이다. 우리는 $L_1$로부터 각 $\sigma$에 대해 $x^{n_2}-\sigma(\alpha_2)^{n_2}$의 splitting field를 구성하는 방식으로 $L_2$를 구성할 수 있으며, Lemma 56.3을 반복 적용하여 각 단계의 확장체의 Galois group over $F$가 항상 solvable임을 알 수 있다.

이제 이 과정을 반복하는데, $i$ 단계에서는 다음과 같은 다항식 $f_i(x)$의 splitting field over $L_{i-1}$을 생각한다.

$$f_i(x) = \displaystyle\prod_{\sigma \in G(L_{i-1}/F)} [x^{n_i} - \sigma(\alpha_i)^{n_i}]$$

최종 단계에서 얻는 체 $L=L_r$는 normal extension of $F$ by radicals이고 $G(L/F)$는 solvable group이다. 또한 구성 방법에서 $K \le L$임을 알 수 있다.

마지막으로, 갈루아 이론에 의해 $G(E/F) \simeq G(L/F)/G(L/E)$ 이다. 따라서 $G(E/F)$는 $G(L/F)$의 factor group이자 homomorphic image이다. $G(L/F)$가 solvable이므로, homomorphic image인 $G(E/F)$ 또한 solvable이다.

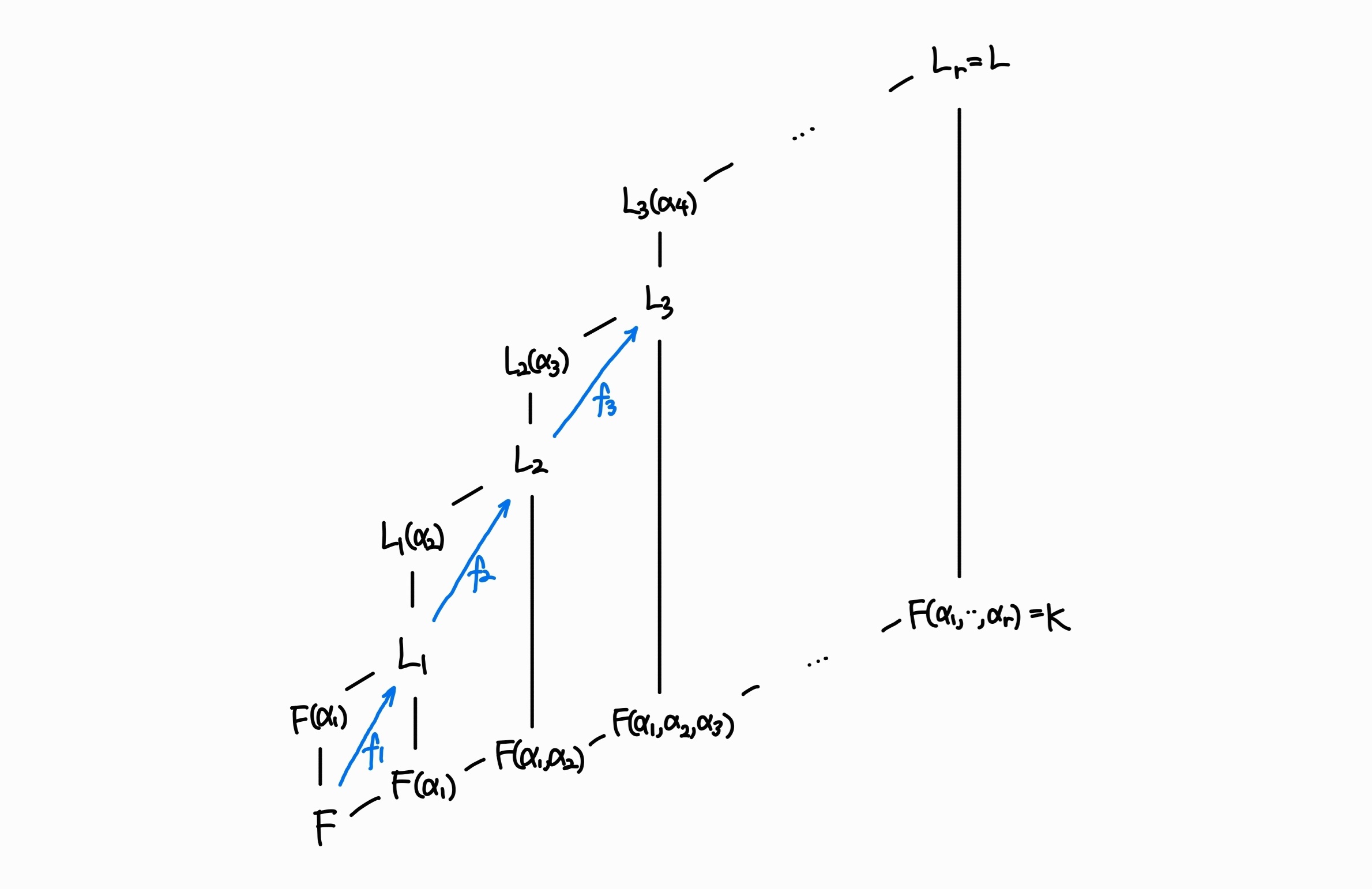확장이 이루어지는 과정

해설. 해당 증명은 체가 확장됨에 따라 세 가지 성질 ① extension by radicals (over $F$), ② normal (of $F$), ③ solvable ($G(\cdot/F)$)이 어떻게 계속해서 전달되는지를 중점으로 보면 큰 틀이 보인다.

1. 우선 ① extension by radicals부터 살펴보자. 즉, 각 $i$에 대해 $L_i$가 extension by radicals over $F$인지를 보자는 것인데, 이는 자명하다. 각 $L_i$를 구성할 때 $L_{i-1}$에다가 $x^{n_i} - \sigma(\alpha_i)^{n_i}$의 근들, 즉 radicals만을 추가하고 있기 때문이다. 따라서 $F$에서부터 시작해 radicals만 추가해 $L=L_r$을 만들 수 있으며, $L=L_r$이 extension by radicals over $F$임을 알 수 있다.

2. 다음으로 ② normal 을 살펴보자. 우리는 새롭게 구성한 확장체들 $L_i$가 $F$의 normal extension이 되기를 원한다. 그래야 Galois group $G(L_i/F)$에 대해 논할 수 있기 때문이다. 여기서 $f_1(x) = x^{n_1}-\alpha_1^{n_1}$으로 정의된 이유를 추측해볼 것이다. 우선 $L_1$을 구성하는 가장 간단한 방법으로 $F$에 $\alpha_1$을 추가한 $F(\alpha_1)$을 생각해볼 수 있다. 그러나 이 체는 normal of $F$가 아니다.

   $F$의 확장체가 normal over $F$이기 위해서는 정의에 의해 splitting field이고 separable extension이라는 조건을 만족해야 한다. $F$가 char $0$ 이므로 separable은 자동으로 충족되고, splitting field인지만 생각하면 된다. 이 때 계수가 $F$에 들어와야 되므로 상수항은 $\alpha_1^{n_1}$을 써야 하고, 다항식이 $\alpha_1$을 근으로 가져야 하므로(그래야 $F(\alpha_n)$을 포함한다), 가장 자연스러운 다항식은 $x^{n_1}-\alpha_1^{n_1}$이 된다. 이제 $L_1 = \text{split}(f_1 (x)/F)$로 정의하면 $L_1$은 $F$의 normal extension이 된다.

   또 다른 질문으로, $f_2 (x) = x^{n_2} - \alpha_2^{n_2} \in L_1[x]$로 정의하지 않은 이유가 무엇일까? 이렇게만 정의해도 $L_2 = \text{split}(f_2(x)/L_1)$가 $L_1$의 normal extension이 되지 않는가? 이에 대한 대답은, “normality”는 추이성이 성립하지 않으므로 $L_2$가 $F$에 대해 normal임이 보장되지 않기 때문이다. 그래서 $\sigma \in G(L_1/F)$를 통해 계수를 $F$에 속하게 만들어주어 $L_2/F$가 normal이도록 보장해준 것이다.

3. 마지막으로 ③ solvable 을 살펴보자. 우선 $G(L_1/F)$가 solvable 인것은 Lemma 56.3에 의해서 바로 보여진다. 이제 $G(L_2/F)$가 왜 solvable이 되는지 자세하게 증명해보자. 각 $\sigma_j$ ($1 \le j \le m=|G(L_1/F)|$)에 대해 $x^{n_2}-\sigma(\alpha_2)^{n_2}$의 splitting field로 확장하는 과정을 수열로 나타내보면 다음과 같다.

   $$L_1 = H_0 < H_1 < H_2 < \cdots < H_{m-1} < H_m = L_2$$

   핵심은 연속된 두 체 $H_{j-1}, H_j$에 대하여 $G(H_{j-1}/F)$가 solvable이면 $G(H_j/F)$도 solvable이라는 것이다. 일단 $H_{j-1}$에서 $H_j$를 구성할 때 Lemma 56.3에 의해 $G(H_j/H_{j-1})$가 solvable임이 보장된다. 또한 (②에서의 논의에 의해) $H_j/F$가 normal이므로 $G(H_j/F)$를 논할 수 있는데, series $\{\iota\} < G(H_j/H_{j-1}) < G(H_j/F)$ 에서 인접한 군들의 몫군 $G(H_j/H_{j-1})/\{\iota\} \simeq G(H_j/H_{j-1})$와 $G(H_j/F)/G(H_j/H_{j-1}) \simeq G(H_{j-1}/F)$가 둘 다 solvable이므로 $G(H_j/F)$ 또한 solvable group이 된다. 따라서 $G(H_{j-1}/F)$가 solvable이면 $G(H_{j}/F)$도 solvable임을 알 수 있다.

   위 과정을 $j=1$부터 $j=m$까지 반복하면 $G(L_1/F)$이 solvable임으로부터 $G(L_2/F)$이 solvable임을 알 수 있다. 그리고 다시 이 과정을 반복하여 모든 $i$에 대해 $G(L_i/F)$이 solvable이라는 것을 알 수 있다.

이렇게 체가 확장됨에 따라 세 가지의 성질이 어떻게 전달되는지 살펴보았다.

수학 공부법 업데이트

이번에 현대대수학을 추가로 공부하면서 수학 공부법도 더욱 발전했다. 구체적인 방법은 다음과 같다.

1. 우선 공부를 할 범위를 선택하고 공부 일정을 산출한다.

   나는 보통 서울대학교 강좌의 강의계획표를 참고해 한 학기 강좌를 4주 분량으로 편성하는 편이다. 이제 일주일 단위로 쪼개어 다음과 같은 과정을 반복한다.

2. 우선 1주 분량에 해당하는 내용을 쭉 훑는다. 증명을 읽어도 되지만 약간 막힌다 싶으면 과감하게 넘어간다. (본문의 20% 이해하는 수준)

   이 단계의 목표는 교재의 전체적인 흐름을 느끼는 것이다. 만약 내용이 이해가 되지 않는다면 그냥 뇌 빼고 읽어도 좋다. 어떤 정리들이 자주 등장하는지, 배운 개념들로 무엇을 계산할 수 있는지만 대충 알아도 큰 도움이 된다.

   보통 이 단계에서는 무지막지하게 졸음이 쏟아진다. 내 생각에는 뇌가 처음보는 내용들 사이에 연관성을 찾아내기 위해 엄청나게 노력하느라 과부하가 걸리기 때문인 것 같다.

3. 다시 본문을 처음부터 차근차근 읽는다. 2단계에 비해서는 증명도 좀 꼼꼼히 읽어보고, 이해가 안되는 부분에서 고민도 좀 해본다. 그렇다고 해서 완전히 이해할 필요는 없고, 너무 어려운 내용은 적당히 넘어간다. (본문의 50% 이해하는 수준)

   이제 어느정도 본문이 이해가 되었다 싶으면 연습문제를 풀어본다. 다만 안풀리는 문제가 있을 경우 너무 오래 붙잡고 있지 말고 10~20분만 풀어보고 과감하게 넘어갈 것.

4. 이제 전체적인 흐름은 이해가 된 상태이다. 이제 모든 정리와 증명을 완벽하게 이해하면서 읽는다. (본문 100% 이해하는 수준)

   그리고 못 푼 연습문제가 있다면 꾸준히 풀이를 시도해본다.

그리고 다음은 알고 있으면 도움이 되는 공부법 꿀팁들이다.

1. 본문의 난이도에 따라 공부 방법에 약간의 변화를 줘도 괜찮다. 이를테면,

• 쉬운 난이도인 경우: 그냥 본문을 한번만 읽은 후에 바로 연습문제를 풀기 시작한다.
• 보통 난이도인 경우: 위에서 설명한 방법과 동일하게 공부하면 된다.
• 어려운 난이도인 경우: 본문이 어려운 경우에는 연습문제도 어려운 경우가 많다. 특히 어려운 연습문제의 경우 3번 풀어보고 답지를 봤는데도 그 풀이가 이해가 안될 때가 있다. 이때가 정말 비상인데, 내용을 더 읽거나, 그 문제만 째려보는 식으로 최대한 이해하기위해 노력해보자.

2. 40분을 연속으로 공부한 후에는 5분 이상 환기하자. 이 과정을 통해 뇌를 다시 환기시킬 수 있다.

3. 안 풀리는 연습문제의 경우 3번 이상 풀어본 다음 답을 보자. 이 때 문제 풀이 시도는 모두 다른 날짜에 이루어져야 한다. 즉, 3일에 걸쳐 3번 풀어보고 해설을 참고하자.

   어느정도 고민한 후에는 답지를 보는 것도 나쁘지 않다고 생각한다. 그 해설을 통해서도 개념의 이해도를 높일 수 있기 때문이다.

마무리하며

이렇게 2달에 걸친 현대대수학 공부가 막을 내렸다. 그동안 궁금증을 가지고 있었던 3대 작도 불능 문제나 5차 방정식의 근의 공식과 같은 흥미로운 주제들을 다룰 수 있어 매우 재미있었다. 또한 현대대수를 공부하며 새로운 학습 방식을 개발하는 등 스스로도 한 단계 성장한 것 같아 뿌듯하다.

현재 계획으로는 우선 학부 3학년 과목에 해당하는 복소해석학, 현대대수학, 미분기하학, 위상수학을 먼저 끝내는 것이 목표이다. 이들은 심화 수학의 기초가 되는 과목들이기 때문이다. 그 이후에 수리논리학, 함수해석학, 미분대수학, 범주론 등 관심있는 분야들을 차례대로 공부해보고자 한다.

이제 미분기하학을 공부하러 가야겠다.