Fraleigh 현대대수학 1 탐구 노트

개요

저는 그동안 Fraleigh 현대대수학 교재 전반부를 공부했습니다.
현대대수학 1 파트에서 중요하다고 느낀 개념들, 깊이 고민해본 주제들을 기록하려고 합니다.

이 글은 현대대수학 1을 처음 접하는 사람들에게 적합하지 않습니다.
현대대수학을 이미 공부하고 있지만 일부 개념이 모호하게 느껴지시는 분들이나, 복습을 통해 내용을 정리하고 싶은 분들에게 적절한 글입니다.

이 글에서 다루는 주제는 다음과 같습니다.

Chapter 14~15, 26~27: Homomorphism과 Factor Group/Ring 구조의 확장
Chapter 21: Integral Domain과 Field of Quotients의 포함 관계
Chapter 22: Polynomial의 본질과 Indeterminate의 의미
Chapter 31: Finite Extension과 Algebraic Extension 사이의 관계

Homomorphism과 Factor Group/Ring 구조의 확장

우선 factor group을 정의하는 이유에 대해서 한번 생각해보겠습니다. 저희는 13장에서 homomorphism(준동형 사상)에 대해 배웠습니다. Homomorphism $\phi:G→G'$ 는 $G$ 를 $G'$ 로 보내는 "함수"입니다. 이때 어떤 원소들은 $\phi$ 에 의해 서로 구분되지 않고 뭉쳐져서 같은 값으로 보내집니다. 다음과 같은 예시를 보겠습니다.

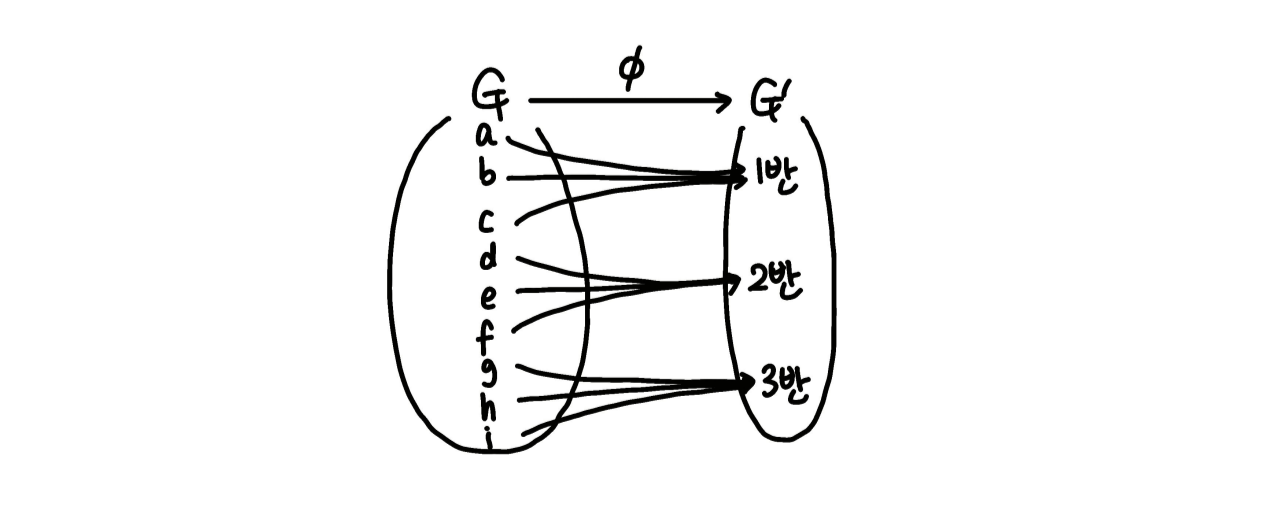각 학생이 몇 반에 속하는지 반환하는 함수

$G$ 는 학생들의 집합, $G'$ 는 반들의 집합, 그리고 $\phi$ 는 어떤 학생을 받아서 그 학생이 몇 반인지를 반환하는 함수입니다. 이 때 $\phi$ 를 보면, $G$ 의 원소들이 $G'$ 에서 구별되지 않는 경우가 생깁니다. $\phi$ 가 본질적으로 보존하지 않는 차이가 있다는 것입니다. 그렇다면 굳이 같은 상으로 가는 원소들을 따로따로 다룰 필요가 없습니다. 구분 불가능한 원소들을 묶어서 하나로 보겠습니다.

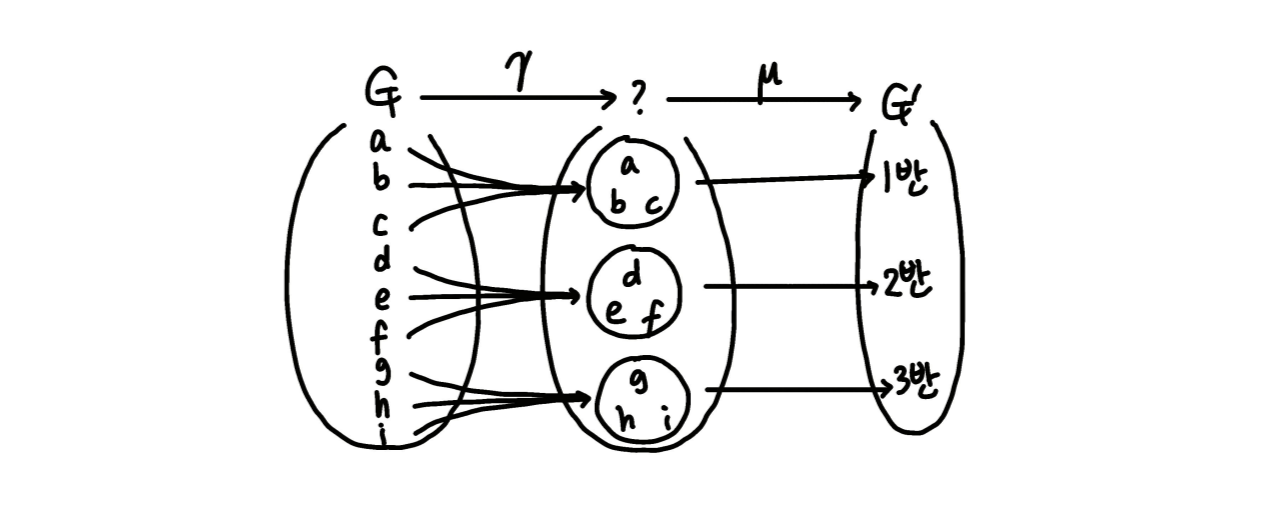중간에 새로운 층을 추가하였다

처음 그림에서 중간에 층이 하나 더 생겼습니다. 가운데 집합은 $G$ 에서 같은 상을 가지는 원소들을 묶은 집합들을 모은 집합입니다. 첫 번째 사상을 $\gamma$ , 두 번째 사상을 $\mu$ 라고 하겠습니다. 그림에서 볼 수 있듯이 $\mu$ 는 isomorphism입니다. $\phi$ 의 특성은 모두 $\gamma$ 에 녹아들어 있으며, 이제는 굳이 $G'$ 를 바라보지 않아도 $\phi$ 의 모든 구조를 $G$ 안에서 설명할 수 있게 되었습니다.

이 가운데 집합이 바로 $G/H$ 입니다.

Theorem 14.11 (The Fundamental Homomorphism Theorem)
Let $\phi: G \to G'$ be a group homomorphism with kernel $H$ . Then $\phi[G]$ is a group, and $\mu: G/H \to \phi[G]$ given by $\mu(gH)=\phi(g)$ is an isomorphism. if $\gamma: G \to G/H$ is the homomorphism given by $\gamma(g)=gH$ , then $\phi(g)=\mu \gamma(g)$ for each $g$ in $G$ .

지금은 준동형사상 $\phi$ 의 Kernel에 대해서만 몫군 $G/H$ 를 정의하였습니다. 이제 확장을 위해 이것이 가능했던 이유를 수학적으로 자세히 살펴보겠습니다. $G/H$ 가 군이 되기 위해서는 다음과 같은 연산이 잘 정의되어야 합니다.

(aH)(bH)=(ab)H

위와 같은 연산이 잘 정의된다고 가정하면 임의의 $a \in G$ 에 대해 $aH=Ha$ 를 얻습니다. 왜냐하면 임의의 $x \in aH$ 에 대해 $(xH)(a^{-1}H)=(x a^{-1} )H$ 이고 $(aH)(a^{-1}H)=eH=H$ 가 되어서 $x a^{-1} \in H$ , 즉 $x \in Ha$ 를 얻기 때문입니다.
반대로 $aH=Ha$ 가 모든 $a \in G$ 에 대해 성립한다고 가정하겠습니다. 각 집합 $aH, bH$ 에서 대표원을 $a h_1 \in aH, b h_2 \in bH$ 와 같이 뽑으면 $(a h_1)(b h_2) = a(h_1 b)h_2 = a(b h_3)h_2 = (ab)(h_3 h_2)$ 입니다. 따라서 $(aH)(bH)=(ab)H$ 가 성립함을 알 수 있습니다.

결국 모든 $g \in G$ 에 대해 $gH=Hg$ 만 성립하면 몫군 $G/H$ 를 정의할 수 있습니다. 이러한 조건을 만족하는 부분군 $H$ 를 normal group(정규군)이라고 합니다. 참고로 $\text{Ker}(\phi)$ 는 이 조건을 항상 만족합니다.

Chapter 15. Factor-Group Computations and Simple Groups

두 가지의 새로운 개념이 나옵니다.
첫 번째는 simple group(단순군)입니다.

Definition 15.14
A group is simple if it is nontrivial and has no proper nontrivial normal subgroups.

두 번째는 maximal normal subgroup(최대 정규부분군)입니다.

Definition 15.17
A maximal normal subgroup of a group G is a normal subgroup M not equal to G such that there is no proper normal subgroup N of G properly containing M.

이름만 보고 대충 감을 잡아보면 단순군은 더 이상 작은 것이 없는 군이고, 최대 정규부분군은 더 이상 큰 것이 없는 군입니다. 저는 이 흐름이 자연수의 약수 관계와 비슷하다고 느꼈습니다.

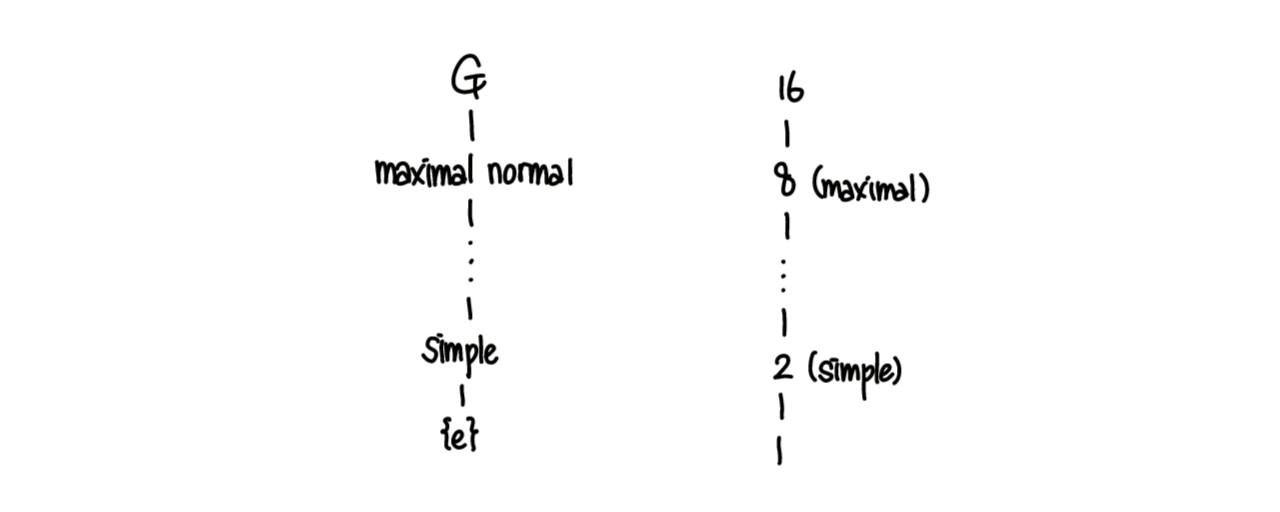Cayley Diagram으로 그린 군의 관계. 예시로 든 16의 그래프와 함께 그렸다.

16의 약수들을 가지고 위 내용을 비유해보았습니다. 최대 정규부분군은 이를테면 16의 진약수 중에서 가장 큰 8입니다. 16을 8로 나누면 2가 나오고, 2는 1보다 큰 약수를 가지지 않습니다. simple하다고 할 수 있겠습니다.

실제로 군에서도 maximal normal subgroup과 simple group 사이에 비슷한 성질이 성립합니다.

Theorem 15.18
$M$ is a maximal normal subgroup of $G$ if and only if $G/M$ is simple.

우선 $M$ 이 maximal normal subgroup인 경우를 살펴보겠습니다. 만약 $G/M$ 의 nontrivial proper normal sugroup이 존재한다면, 이 군의 $\gamma^{-1}$ 은 $M$ 을 properly하게 포함하는 $G$ 의 proper normal subgroup이 됩니다. 이는 $M$ 이 maximal임에 모순입니다.

반대로 $G/M$ 이 simple인 경우에도 $M$ 이 maximal이 됩니다. 왜냐하면 $M$ 을 properly하게 포함하는 $G$ 의 normal subgroup $N$ 이 존재한다면 $\gamma[N]$ 은 $G/M$ 의 nontrivial proper normal subgroup이 되어 모순이기 때문입니다. 따라서 $M$ 은 maximal입니다.

이 과정을 한눈에 볼 수 있게 그림으로 나타내면 아래와 같습니다.

N과 γ[N]로부터 모순을 이끌어 내는것이 증명의 핵심이다

Chapter 26. Homomorphisms and Factor Rings

이제 환에서 homomorphism을 가지고 똑같은 이야기를 하기 위해 ring을 쪼개는 factor ring을 정의합니다. 달라진 점은 곱하기 연산 " $\cdot$ " 하나가 추가되었다는 것 뿐입니다. 이 때 Factor Ring이 환이 되기 위해서는 아래와 같은 덧셈과 곱셈이 잘 정의되어야 합니다.

(a+H)+(b+H)=(a+b)+H, \quad (a+H)(b+H)=ab+H

첫 번째 조건은 덧셈의 교환 법칙에 의해서 당연히 성립합니다. 두 번째 조건을 살펴보기 위해 대표원을 골라 전개해보면 $(a+h_1)(b+h_2)=ab+a h_2+h_1 b+h_1 h_2$ 이 됩니다. 우변이 $ab+H$ 에 속하기 위해서는 $a h_2+h_1 b+h_1 h_2 \in H$ 이어야 합니다. $h_1 h_2 \in H$ 임은 자명하고, 결국 $aH \subset H, Hb \subset H$ 이어야만 합니다. 반대로 이 조건을 만족하면 항상 곱셈 $(a+H)(b+H)=ab+H$ 이 잘 정의됨을 살펴볼 수 있습니다.

factor ring이 잘 정의될 필요충분조건인 $aH \subset H, Hb \subset H$ 을 만족하는 additive subgroup $H$ 를 ideal라고 합니다.

Chapter 27. Prime and Maximal Ideals

해당 챕터에서는 세 가지의 중요한 정리가 등장합니다.

For a commutative ring $R$ with unity:

An ideal $M$ of $R$ is maximal if and only if $R/M$ is a field.

An ideal $N$ of $R$ is prime if and only if $R/N$ is an integral domain.

Every maximal ideal of $R$ is a prime ideal.

2, 3번 정리는 비교적 간단하게 증명할 수 있으므로 1번 정리에 대해 자세히 살펴보겠습니다. maximal이라는 단어를 보면 위에서 다루었던 Theorem 15.18이 떠오릅니다. maximal ideal M으로 R을 자르면 뭔가 simple ring이 나와야 할 것 같은데, 왜 갑자기 field가 나온 것일까요? 다음 연습문제를 보면 그 관계를 더 쉽게 파악할 수 있습니다.

Exercise 27.29
Show that $N$ is a maximal ideal in a ring $R$ if and only of $R/N$ is a simple ring, that is, it is nontrivial and has no proper nontrivial ideals.

저희가 예상했듯이, 어떤 ring을 그것의 maximal ideal로 자르면 simple ring이 나옵니다. 증명은 Theorem 15.18과 아주 유사합니다. 여기에 $R$ 이 commutative ring with unity라는 조건이 추가되었기 때문에 $R/N$ 이 field가 된 것입니다. 이는 다음과 같이 논증할 수 있습니다.

$R$ 이 commutative이므로 $R/N$ 도 자동으로 commutative가 됩니다. 이제 $R/N$ 의 임의의 원소 $x \neq 0$ 이 unit임만 보이면 됩니다. principal ideal $\lang x \rang \subset R/N$ 을 생각하면 $R/N$ 이 simple이므로 $\lang x \rang$ 으로 가능한 것은 $\{0\}$ 과 $R/N$ 뿐입니다. 그러나 $x \neq 0$ 에서 $\lang x \rang\neq \{0\}$ 이므로 $\lang x \rang = R/N$ 이며, 어떤 $y \in R/N$ 이 존재하여 $xy=1$ 이 됩니다. 따라서 $x$ 은 unit입니다.

결국 환에서의 homomorphism과 factor ring의 이야기들은 Chapter 14~15에 걸쳐 다루었던 군의 homomorphism과 factor group 이야기의 자연스러운 확장임을 알 수 있습니다.

Integral Domain과 Field of Quotients의 포함 관계

Chapter 21. The Field of Quotients of an Integral Domain

해당 챕터에서는 integral domain $D$ 로부터 체를 만드는 방법을 서술합니다. 체로 만들어주기 위해서는 모든 원소가 unit이 되도록 해주어야 하는데, 분자와 분모가 $D$ 의 원소인 "분수" 꼴로 생각하여 이 문제를 해결합니다. 더욱 엄밀하게 서술하면 다음과 같습니다.

집합 $S$ 를 $S = \{ (a,b) \, | \, a,b \in D, b \neq 0\}$ 와 같이 정의한다.
집합 $S$ 에서의 동치관계 $\sim$ 을 $(a,b) \sim (c,d) \iff ad=bc$ 과 같이 정의한다.
이제 $F = \{ [(a,b)] \, | \, (a,b) \in S \}$ 라고 한다.
$F$ 에서의 덧셈과 곱셈을 $[(a,b)]+[(c,d)]=[(ad+bc, bd)], [(a,b)][(c,d)]=[(ac,bd)]$ 로 정의한다.
$F$ 는 덧셈에 대한 항등원이 $[(0,1)]$ 이고 곱셈에 대한 항등원이 $[(1,1)]$ , $[(a,b)]$ 의 역원이 $[(b,a)]$ 인 체가 된다.

이렇게 체 $F$ 를 구성하고 나면, 사실상 $D$ 는 $F$ 에 포함되는 것처럼 간주할 수 있습니다. 왜냐하면 사상 $i: D \to F$ 를 $i(a) = [(a,1)]$ 와 같이 정의하면 isomorphism이 되기 때문입니다. 그리고 교재에서는 $D$ 가 $F$ 의 부분집합인 것으로 간주하고 논의를 전개합니다...?

저는 이 부분을 납득하지 못하겠습니다. $D$ 가 $F$ 안에 자연스럽게 흡수되는 것은 맞지만, 실제로 " $D \subset F$ "라고 표기하는 것은 수학적으로 틀린 명제이기 때문입니다. 차라리 위의 논의에서는 " $D$ 의 원소를 모두 포함하는 체 $F$ 가 존재한다"는 결론을 도출하는 것이 더욱 합리적입니다. 물론 편리함을 위해서 약간의 엄밀함을 포기했다고 볼 수는 있지만, 이 간단한 가정 하나 때문에 수학적으로 엄밀하지 않은 문장이 우후죽순 생겨나게 됩니다.

엄밀하지 않은 부분들을 빨간색으로 표시하고 수정하였다

이후에 이 부분을 반복해 읽으면서 $D \subset F$ 와 같은 표기가 데려다주는 편리함이 매우 크다는 것을 어느정도 이해하게 되었지만, 엄밀성의 부재에 대한 불편함을 완전히 떨쳐내지는 못하였습니다. 앞으로도 엄밀함과 편리함중에 어느 것을 선택해야 하는지에 대해 계속 고민해야 할 것 같습니다.

Polynomial의 본질과 Indeterminate의 의미

Chapter 22. Rings of Polynomials

22장부터는 다항식에 대한 이야기를 전개합니다. 어떤 다항식이 주어진 체 안에서 해를 가지는지, 그리고 가지지 않는다면 해를 가지도록 체를 확장할 수 있는지 여부 등을 알고 싶기 때문입니다. 이러한 이야기를 하기 위해서는 우선 다항식을 정의하고 넘어가야 합니다.

그러나 이러한 다항식들을 다룰 때 $x$ 가 값을 가지는 변수라고 생각하면 굉장히 헷갈립니다. 책에서는 이를 variable이 아닌 indeterminate라고 부름으로써 구분합니다. 제 직관을 약간 더 더해 설명하자면, 덧셈과 곱셈이 다항식처럼 정의된 수열이라고 생각하면 편합니다. 즉 아래와 같이 생각하자는 것입니다.

a_0 + a_1 x + a_2 x^2 + a_3 x^3 + ... \; := \; (a_0, a_1, a_2, a_3, ...)

이러한 수열들의 덧셈과 곱셈이 다항식과 동일하게 작용하기 때문에 계산과 표기의 편리함을 위해 변수 $x$ 를 사용한 것이지, $x$ 는 아무 의미를 가지지 않는 기호일 뿐입니다. 따라서 환 $R$ 의 원소들을 계수로 하는 다항식들의 집합을 $R[x]$ 가 아닌 $R[\,]$ 라고 적겠습니다. 또한 각각의 다항식은 $f(x)$ 대신 $f()$ 라고 표기하겠습니다.

예를 들어 다항식 $f(x)=x^2+2$ 에서 변수 $x$ 는 그냥 허상일 뿐이며, 실제로는 아래와 같은 수열로 생각해야 합니다.

f()= (2,0,1,0,0,0,0,...)

여기서 표기의 편리함을 위해 끝없이 이어지는 $0$ 은 무시하고 $(2,0,1)$ 이라 쓰겠습니다.

이러한 관점에서 봤을 때 $\alpha \in E$ 의 evaluation homomorphism $\phi_\alpha$ 는 어떤 수열 $(a_0,a_1,a_2,...) \in F^\omega$ 를 받아서

\phi_\alpha((a_0, a_1, a_2, ...)) = a_0 \cdot \alpha^0 + a_1 \cdot \alpha^1 + a_2 \cdot \alpha^2 + ...

을 반환하는 함수일 뿐입니다. 이 때 $a_i$ 들이 들어있는 $F$ 와, $\alpha$ 가 들어있는 $E$ 에는 다음과 같은 이항 연산들이 잘 정의되어 있어야 합니다.

$\cdot: E \times E \to E$ ( $\alpha^n$ 의 계산을 위해)
$\cdot: F \times E \to E$ ( $a_i \cdot \alpha^n$ 의 계산을 위해)
$+: E \times E \to E$ (위 항들의 합 계산을 위해)

실제 예시를 통해 이해해보겠습니다.

$\phi_2 (x^2+2)$

이 경우에 다항식의 계수가 들어있는 $\mathbb{Q}$ 와 $\alpha=2$ 가 들어있는 $\mathbb{R}$ 에는 위에서 언급한 이항 연산들이 잘 정의되어 있습니다. 따라서
$\phi_2 (x^2+2) = \phi_2((2,0,1)) = 2 \cdot 2^0 + 0 \cdot 2^1 + 1 \cdot 2^2 + 0 \cdot 2^3 + ... = 6$
임을 쉽게 알 수 있습니다.
$\phi_\alpha (x^2+1)$ (단, $\alpha = x+ \lang x^2+1 \rang$ )

이 때 $\alpha$ 를 정의하는 식에서의 $x$ 또한 어떤 수가 들어가는 변수가 아니라, 그냥 수열을 나타내는 기호일 뿐입니다. 다시 말해
$\alpha = x+\lang x^2+1 \rang = \{(1,) + (a_0, a_1, a_2, ...) \cdot (1, 0, 1) \;|\; (a_0, a_1, a_2, ...) \in F[\,] \}$
와 같이 생각해야 합니다. 그러면 저희가 잘 알고 있듯이 $F=\mathbb{Q}$ 와 $E=\mathbb{Q}[\,]$ 에는 위에서 언급한 이항 연산들이 잘 정의되어 있고, 따라서
$\begin{equation*} \begin{split} \phi_\alpha (x^2+1) &= \phi_\alpha((1,0,1)) = 1 \cdot \alpha^0 + 0 \cdot \alpha^1 + 1 \cdot \alpha^2 + 0 \cdot \alpha^3 + ... = \alpha^2 + 1 \\ &= (x+ \lang x^2+1 \rang)^2+1 = x^2 + \lang x^2+1 \rang + 1 = \lang x^2+1 \rang = 0 \end{split} \end{equation*}$
과 같이 계산할 수 있습니다.

이렇게 다항식을 수열로 이해하면 개념이 더욱 명확해지는 것을 알 수 있습니다.

p. 198
우리는 $x^2-4=0$ 와 같은 식은 절대 적지 않을 것이다. 왜냐하면 단순히 ring $\mathbb{Z}[x]$ 에서 $x^2-4$ 는 zero polynomial이 아니기 때문이다.

22장의 서론 부분에서 위와 같은 내용이 있는데, 이는 우리의 관점에서 보았을 때 $x^2-4 = (-4,0,1)$ 이고, $0=(0,)$ 이므로 서로 같지 않은 것은 당연합니다.

다만 상수항과 관련해서는 약간의 주의가 필요합니다. 이 교재에서는 $F$ 의 원소 $a$ 와 $F[x]$ 의 상수항 $a$ 를 구분하지 않습니다. 일례로 Kronecker's Theorem (Theorem 29.3)의 증명을 보면 $F$ 에서 $F[x]/ \lang p(x) \rang$ 로의 함수 $\psi: F \to F[x]/ \lang p(x) \rang$ 를 $\psi(a) = a + \lang p(x) \rang$ 와 같이 정의합니다. 그리고 $\psi$ 가 단사임을 증명할 때에도 " $a+\lang p(x) \rang = b + \lang p(x) \rang$ 에서 $(a-b) \in \lang p(x) \rang$ 이고, $a-b \in F$ 는 차수가 $1$ 이상인 $p(x)$ 의 배수이므로 $a-b=0$ 이다" 와 같이 논의를 전개합니다.

그러나 제가 작성한 다항식의 정의를 엄격하게 적용한다면, 함수 $\psi: F \to F[\,]/ \lang p() \rang$ 는 $\psi(a) = (a,) + \lang p() \rang$ 와 같이 정의되어야 할 것입니다. 물론 표기만 약간 바뀔 뿐 증명의 흐름은 똑같이 따라갈 수 있습니다.

Finite Extension과 Algebraic Extension 사이의 관계

Chapter 31. Algebraic Extensions

해당 챕터에서는 두 가지 종류의 extension을 정의합니다. $F$ 에 대해서 대수적인 수들만 모여있는 algebraic extension과, $F$ 에 대해서 vector space로 보았을 때 finite dimension을 가지는 finite extension입니다. 이 둘은 물론 서로 밀접한 관계를 가지고 있습니다.

Theorem 31.3
A finite extension field $E$ of a field $F$ is an algebraic extension of $F$ .

우선 모든 finite extension은 algebraic extension입니다. 이는 30장에서 배운 벡터공간을 응용하면 쉽게 알 수 있습니다. $[E:F]=n$ 일 때 각 $\alpha \in E$ 에 대하여 $1, \alpha, ..., \alpha^n$ 은 선형 종속이고, 따라서 그 계수들을 사용해 $f(\alpha)=0$ 인 다항식 $f(x) \in F[x]$ 를 잡을 수 있습니다. 다시 말해, $\alpha$ 는 $F$ 에 대해 대수적입니다.

Theorem 31.11
Let $E$ be an algebraic extension of a field $F$ . Then there exist a finite number of elements $\alpha_1, ..., \alpha_n$ in $E$ such that $E = F(\alpha_1, ..., \alpha_n)$ if and only if $E$ is a finite-dimensional vector space over $F$ , that is, if and only if $E$ is a finite extension of $F$ .

그러나 모든 algebraic extension이 finite extension인 것은 아닙니다. 예를 들어 $\mathbb{Q}(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, ...)$ 은 $\mathbb{Q}$ 의 algebraic extension이지만 finite extension은 아닌데, 이런 식으로 무한 개의 원소를 추가하여 field extension을 만드는 경우가 있기 때문입니다.
만약 유한 개의 원소만 추가한다면 이는 finite extension이 됩니다. 반대로 finite extension이라면 항상 유한개의 원소 $\alpha_1, ..., \alpha_n$ 을 잡아 $E = F(\alpha_1, ..., \alpha_n)$ 이 되도록 할 수 있습니다.

Theorem 31.4
If $E$ is a finite extension field of a field $F$ , and $K$ is a finite extension field of $E$ , then $K$ is a finite extension of $F$ , and
$[K:F]=[K:E][E:F]$

한편 finite extension은 추이성을 가지고 있습니다. 이는 $E$ 를 $F$ 에 대한 벡터 공간으로 보았을 때의 기저 $\{ \alpha_i \}$ 와, $K$ 를 $E$ 에 대한 벡터 공간으로 보았을 때의 기저 $\{ \beta_j \}$ 에 대해 $\{\alpha_i \beta_j\}$ 가 $K$ 의 기저가 되기 때문입니다. 여기서 기저 벡터의 개수를 세면 $[K:F]=[K:E][E:F]$ 이 성립함도 알 수 있습니다.

그러면 새로운 궁금증이 생깁니다. 만약 algebraic extension에 대해서도 추이성이 성립할까요? 즉 $K$ 가 $E$ 에 대해 대수적이고 $E$ 가 $F$ 에 대해 대수적이면 $K$ 도 $F$ 에 대해 대수적일까요? 직관적으로는 그럴 것 같지만, 위에서 증명한 Theorem 31.4를 바로 적용할 수는 없습니다. 각 algebraic extension이 finite하지 않을 수도 있기 때문입니다. 여기서 제가 소개하고 싶은 기법이 등장합니다. $K$ 의 모든 원소를 한번에 다루려면 finite extension의 원리를 적용할 수 없지만, 각 원소 $\alpha \in K$ 를 하나씩 보면 finite extension의 원리를 적용할 수 있습니다.

Exercise 31.31
Show that if $F$ , $E$ and $K$ are fields with $F \le E \le K$ , then $K$ is algebraic over $F$ if and only if $E$ is algebraic over $F$ , and $K$ is algebraic over $E$ . (You must not assume the extensions are finite.)

증명( $\Larr$ ). 임의의 $\alpha \in K$ 를 선택하자. 우리는 $\alpha$ 가 algebraic over $F$ 임을 보여야 한다. $K$ 가 algebraic over $E$ 이기 때문에, $E[x]$ 에 어떤 다항식 $f(x) = a_0 + a_1 x + a_2 x^2 + ... + a_n x^n$ 이 존재하여 $f(\alpha)=0$ 이다. 또한 $E$ 가 algebraic over $F$ 이므로 각 $a_i$ 들은 algebraic over $F$ 이고, 따라서 $F(a_0, a_1, ..., a_n)$ 은 $F$ 의 finite extension이다. 한편 $f(x) \in E[x]$ 에 의해 $\alpha$ 는 algebraic over $F(a_0, a_1, ..., a_n)$ 이고, 따라서 $F(a_0, a_1, ..., a_n, \alpha)$ 은 $F(a_0, a_1, ..., a_n)$ 의 finite extension 이다. Theorem 31.4에 의해 $F(a_0, a_1, ..., a_n, \alpha)$ 는 $F$ 의 finite extension이고, $\alpha$ 가 algebraic over $F$ 임을 얻는다.

증명에서 사용된 핵심 논리는 $\alpha$ 가 algebraic over $E$ 이고 $E$ 가 algebraic over $F$ 이면 $\alpha$ 가 algebraic over $F$ 라는 것이었습니다. 이 논리는 algebraic closure, algebraically closed 등 다양한 개념과 관련된 문제에서 계속 등장하기 때문에 기억하고 있으면 굉장히 편리합니다.

마치며

이렇게 현대대수학 1을 공부하며 중요하다고 생각된 내용들을 정리했습니다.
앞으로도 공부한 과목들은 이런 식으로 핵심 내용을 간단하게 정리할 예정입니다. 남에게 설명을 하듯이 글을 쓰는 과정에서 단순히 책을 읽는 것보다 훨씬 깊은 이해도를 얻을 수 있기 때문입니다.

앞으로의 공부 계획은 다음과 같습니다. 먼저 집합론은 추석 연휴 안에, 현대대수학 2는 한 달 내에 마무리하는 것을 목표로 하고 있습니다. 이후에는 미분대수학 공부를 통해 최종적으로 $e^{x^2}$ 의 적분이 초등함수로 표현될 수 없는 이유를 공부하고자 합니다.
추가로, 학부 3학년 수학 과목 중에 아직 공부하지 못한 위상수학과 미분기하학 또한 올해 안 혹은 내년 초까지 공부할 계획입니다.