logogeniusLHS 블로그

김홍종 미적분학 2 탐구문제 풀이집 제작기

차세대 조판 소프트웨어 typst, 그리고 재미있는 문제들

2024. 01. 09.
-

개요

6개월 전 저는 김홍종 미적분학 1 탐구문제 풀이집을 만들었습니다. 1학년 2학기에는 고급수학2 강의를 들었으며, 그래서 자연스럽게 미적분학 2 탐구문제에도 도전하게 되었습니다. 오늘은 이 탐구문제 풀이집을 만든 후기 및 재미있는 문제들에 대해서 이야기하려고 합니다.

솔직히 문제를 풀면서 중간에 그만둘까 고민을 많이 했습니다. 미적분학 1 탐구문제의 경우 제 기준에서 난이도가 쉬웠고, 처음부터 "빨간 글씨", 즉 심화된 내용을 다룰려고 풀이집 제작을 시작한 것이었습니다. 그러나 미적분학 2 탐구문제를 풀 때는 문제 이해조차 힘들 때가 있을 정도로 배경지식이나 실력이 부족한 상태였습니다. 그래도 고급수학2 강의를 방금 들은 지금 끝내는게 맞다고 생각해서 많은 질문 및 검색을 통해 완성하게 되었습니다.

제작

조판 소프트웨어 typst

우선 문제를 풀 때는 저번과 마찬가지로 태블릿을 사용했습니다. 그런데 저번처럼 손글씨를 그대로 pdf로 바꿔서 풀이집을 게재하는 것 말고 새로운 도전을 해보고 싶더군요. 바로 조판 소프트웨어를 사용해 문서화 시키는 것입니다. 저는 조판 소프트웨어로 typst를 선택했습니다.

typsttypst

저는 9월 초에 typst를 처음 접한 이후로 학교 수학 과제를 작성할 때 몇 번 사용해봤습니다. 이전까지는 LaTeX밖에 써본적이 없었는데, typst 랜딩 페이지를 훑어본 결과 훨씬 간편하고 간결할 것 같다는 생각이 들었기 때문입니다. 그리고 typst를 사용함에 따라서 그러한 생각은 확신으로 바뀌어갔습니다. 제가 생각하는 typst의 장점은 다음과 같습니다.

1. 간단한 수식 작성

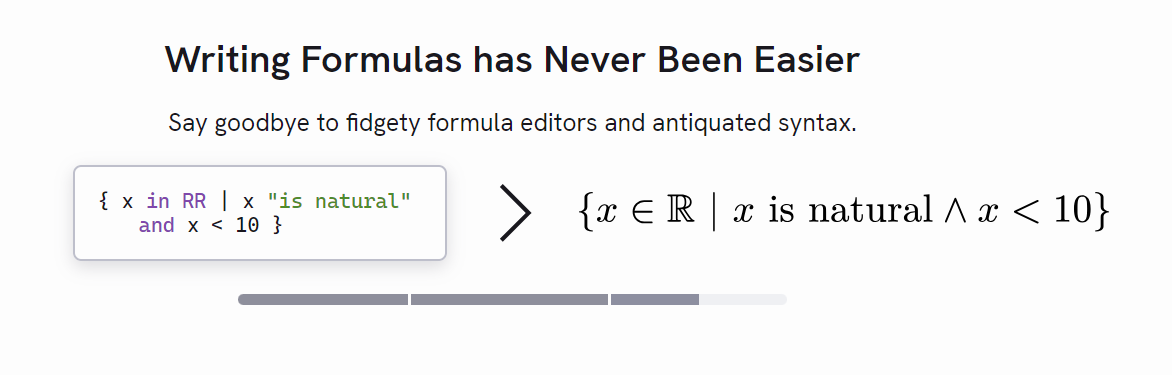간단한 수식 작성간단한 수식 작성

일단 수식을 작성하는 것이 굉장히 간편합니다. LaTeX의 경우 역슬래시를 사용해서 각 문자들을 표현하지만, typst에서는 그럴 필요 없이 단어를 통해 바로 문자를 입력할 수 있습니다. 또한 LaTeX에서는 여러 종류의 화살표를 사용할 때 \leftarrow, \rightrightarrows, \circlearrowright 등 불규칙한 이름을 가지는 반면 typst에서는 arrow.l, arrow.double, arrow.cw 등 같은 arrow 범주에 묶여있어 문자를 찾기가 더욱 편합니다. 분수를 작성할 때도 \frac 같은 명령어 필요 없이 그냥 A/B처럼 쓰면 알아서 처리해줍니다. 이러한 장점은 코드로 적혀있는 수식을 읽을 때 가독성을 더욱 높여줍니다.

2. 굉장히 빠른 컴파일

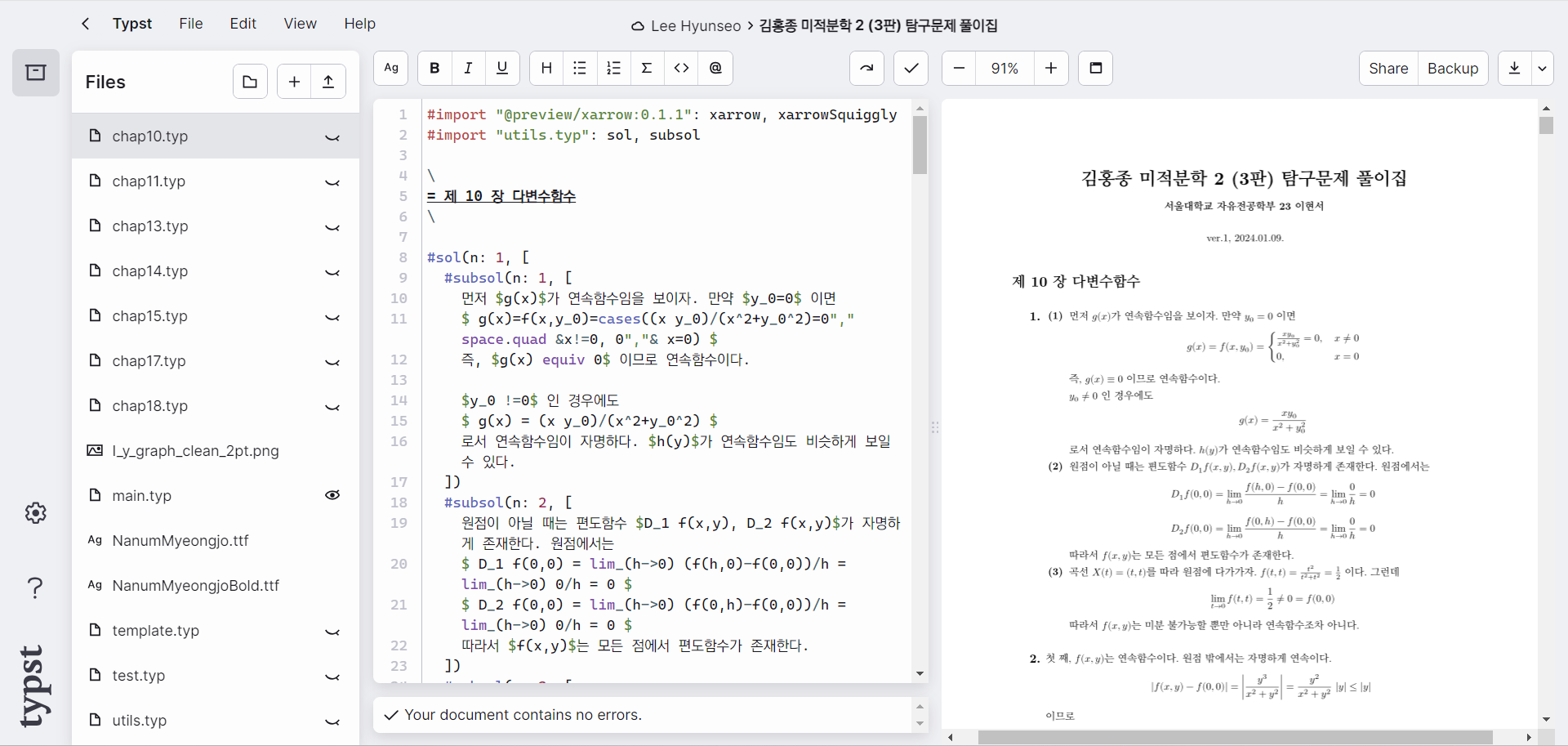typst 온라인 편집기 화면typst 온라인 편집기 화면

위 사진은 typst에서 무료로 제공해주는 온라인 편집기입니다. LaTeX에서의 Overleaf와 비슷한 위치에 있다고 생각하면 될 것 같습니다. 제 기억이 맞다면 Overleaf를 통한 컴파일은 적어도 몇 초가 소요됩니다. 반면 typst에서는 컴파일이 정말 눈 깜짝할 새에 완료됩니다. 즉, 왼쪽에서 글자를 입력함과 동시에 오른쪽에서 미리보기가 가능합니다. 겨우 몇 초 차이지만 수식을 작성함에 있어 바로바로 볼 수 있다는 것은 정말 큰 장점이었습니다. (제가 최근에 LaTeX를 사용해본적이 없어서 컴파일이 몇 초 이상 걸린다는게 사실이 아닐수도 있습니다. 아무리 검색해봐도 한글 폰트가 적용이 안돼서 포기했거든요...)

3. 진짜 프로그래밍 하는 느낌이 듦

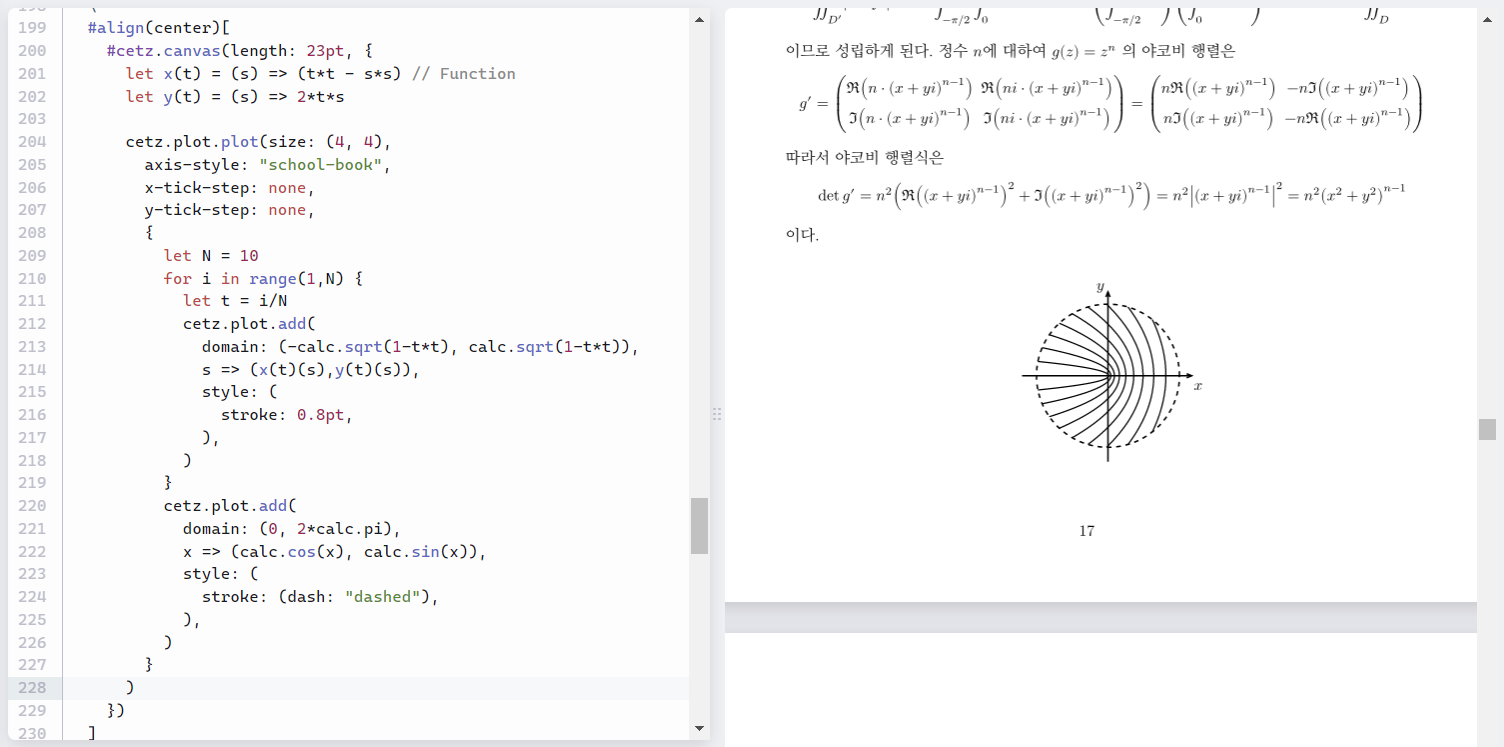typst 온라인 편집기 화면typst 온라인 편집기 화면

이건 그냥 개인적인 생각인데, 진짜 프로그래밍을 하는 것 같은 느낌이 납니다. LaTeX는 역슬래시 때문에 html같은 마크업 언어의 느낌이 강하게 나는데 반해 typst에서 프로그래밍을 할 때는 python과 진짜 비슷하다는 느낌을 많이 받았습니다. 위 사진에서도 for i in range(1,N) 같이 python과 유사한 문법을 사용하고 있습니다. 물론 저는 프로그래밍만 해봤지 LaTeX를 익숙하게 다뤄본 적이 없는 사람이기 때문에 신빙성은 없습니다.

다만 단점이라면, 개인 프로젝트에는 자유롭게 쓸 수 있겠지만 표준이 정해진 논문 등에는 사용할 수 없을 것 같습니다. 아무튼 여러분들도 typst 사용하고 광명 찾으시기 바랍니다.

풀이집 다운로드 페이지

만들어진 풀이집 파일 업로드는 이번에도 Dropbox 서비스를 사용했습니다. 그리고 저번에 사용했던 노션 페이지에 추가해서 링크를 달아놓았습니다. FAQ는 따로 작성하지 않았는데, 딱히 추가할 내용이 없었기 때문입니다. 아, 당연히 오류 제보해주시면 상품을 드릴려고 생각중입니다.

풀이집 다운로드 사이트풀이집 다운로드 사이트

김홍종 미적분학 (3판) 탐구문제 풀이집

위 링크에 들어가시면 풀이집을 구경하실 수 있습니다.

흥미로웠던 문제

미적분학 2 탐구문제 중에서 재밌었던 문제들을 소개하겠습니다.

11장 (최대최소 문제와 고계미분) 7번

좋은 기록이 나오도록 스키장을 건설하려면 어떻게 설계하는 것이 좋을까?

일단 이 문제를 읽으면 가장 먼저 떠오르는 것은 최단강하선 문제입니다. 최단강하선 문제란 수직으로 서있는 평면위의 두 점 사이를 중력에 의해 이동하려고 할 때 가장 적은 시간이 걸리는 곡선을 찾는 문제입니다. 이 문제의 정답은 꽤나 잘 알려져 있는데, 바로 사이클로이드입니다. 따라서 좋은 기록이 나오도록 스키장을 건설하려면 사이클로이드 곡선을 따라 설계하면 될 것입니다.

그러나 이것이 이 문제의 답이라고 할 수 없는게, 저자는 이미 부록에서 변분법과 최단강하선 문제를 다루었습니다. 똑같은 답이라면 굳이 이 문제를 낼 필요가 없을 것입니다. 그렇게 저는 답을 찾기 위해 열심히 인터넷 검색을 하다가 brachistochrone problem with friction(마찰력이 있는 최단강하선 문제) 라는 키워드를 찾았습니다. 그리고 신기하게도 마찰력이 있는 경우에도 곡선의 방정식을 정확히 계산해낼 수 있었습니다.

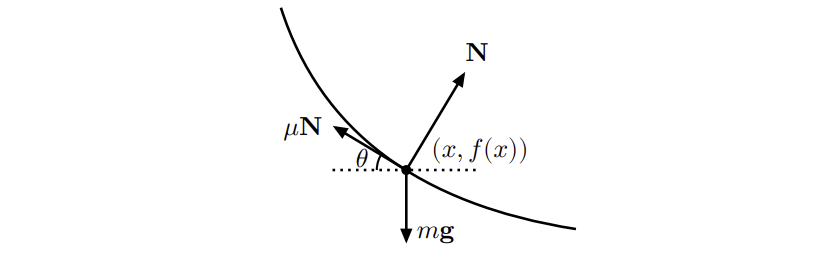상황 분석상황 분석

위 사진과 같은 상황을 생각합니다. 시점은 원점 (0,0)(0,0)이고, 경로는 (x,f(x))(x,f(x))와 같이 나타납니다. 이 때 x>0x>0이면 f(x)<0f(x) < 0입니다. 경사면이 수평선과 이루는 각도를 θ\theta라고 하면 tan⁡θ=−y′\tan \theta = -y'가 성립합니다. 또한 수직항력 N=mgcos⁡θN=mg \cos \theta 이므로 사람이 받는 힘 FF는

F=mgsin⁡θ−μN=mg(sin⁡θ−μcos⁡θ)=ma F=mg \sin \theta - \mu N = mg(\sin \theta - \mu \cos \theta ) = m a

입니다. 또한 다음의 두 식

dvdt=g(sin⁡θ−μcos⁡θ)=g(−y′1+y′2−μ11+y′2)dyds+μdxds=dxds⋅dydx+μdxds=(y′1+y′2+μ11+y′2) \frac{dv}{dt} = g \left(\sin \theta - \mu \cos \theta \right) = g \left(\frac{-y'}{\sqrt{1+{y'}^2}}-\mu\frac{1}{\sqrt{1+{y'}^2}} \right) \\ \frac{dy}{ds} + \mu \frac{dx}{ds} = \frac{dx}{ds} \cdot \frac{dy}{dx} + \mu\frac{dx}{ds} = \left( \frac{y'}{\sqrt{1+{y'}^2}}+\mu \frac{1}{\sqrt{1+{y'}^2}} \right)

에 의해

g(dyds+μdxds)=−dvdt=−dsdt⋅dvds=−vdvds=−12d(v2)ds g \left(\frac{dy}{ds} + \mu \frac{dx}{ds} \right) = -\frac{dv}{dt} = -\frac{ds}{dt} \cdot \frac{dv}{ds} = -v\frac{dv}{ds} = -\frac{1}{2} \frac{d(v^2)}{ds}

이므로 dds(gy+μgx+12v2)=0\frac{d}{ds}(gy+\mu gx+\frac{1}{2}v^2)=0입니다. 초기 상태에서 y=x=v=0y=x=v=0이고, 따라서 gy+μgx+12v2gy+\mu gx+\frac{1}{2}v^2의 값은 항상 00으로 일정합니다. 즉, v=−2g(y+μx)v=\sqrt{-2g(y+\mu x)}입니다. 낙하 시간은

T=∫dt=∫dsv=∫0a1+y′2−2g(y+μx)dx T=\int dt = \int \frac{ds}{v} = \int_{0}^{a} \frac{\sqrt{1+{y'}^2}}{\sqrt{-2g(y+\mu x)}} dx

로 구할 수 있습니다. 이제 이 TT가 최소가 되는 함수 yy를 구해야 하므로 오일러-라그랑주 방정식을 사용합니다. 해당 방정식은 11장 탐구문제 5번에서 다루고 있습니다. 5번의 증명은 풀이집에 있습니다.

이급함수 L(x,y,z)L(x,y,z)에 대하여 공간 F={f∈C2[a,b] ∣ f(a)=ya,f(b)=yb}\mathcal{F}=\{f \in \mathcal{C}^2 [a,b] \, \vert \, f(a)=y_a, f(b)=y_b \} 에서 정의된 범함수

L(f):=∫abL(x,f(x),f′(x))dx \begin{equation*} \mathcal{L}(f):=\int_a^b L(x,f(x),f'(x)) dx \end{equation*}

의 오일러-라그랑주 방정식(L\mathcal{L}이 최소가 되는 ff가 만족하는 식)은

D2L(x,f(x),f′(x))=ddxD3L(x,f(x),f′(x)) \begin{equation*} D_2 L(x,f(x),f'(x)) = \frac{d}{dx} D_3 L(x,f(x),f'(x)) \end{equation*}

임을 보여라.

따라서 L(x,y,z)=1+z2/−2g(y+μx)L(x,y,z)=\sqrt{1+z^2}/\sqrt{-2g(y+\mu x)} 로 두고 위의 방정식을 적용하면 되겠습니다. 꽤나 수식이 복잡해서 자세한 계산과정은 역시 풀이집을 참고해주세요. 간략한 흐름은 다음과 같습니다. 오일러-라그랑주 방정식의 결과로

(1+y′2)(1−μy′)+2(y+μx)y′′=0(1+{y'}^2)(1-\mu y') + 2(y+\mu x)y'' = 0

을 얻습니다. 이 식을 활용하면

ddx((1+y′2)(y+μx)(1−μy′)2)=0\frac{d}{dx} \left( \frac{(1+{y'}^2)(y+\mu x)}{(1-\mu y')^2} \right) = 0

을 얻고, 따라서 상수 A>0A>0가 존재하여

1+y′2(1−μy′)2=−Ay+μx\frac{1+{y'}^2}{(1-\mu y')^2} = -\frac{A}{y+\mu x}

를 만족합니다. 마지막으로 y′=−cot⁡(θ/2)y'=-\cot(\theta/2)로 치환하면

{x=12A[(θ−sin⁡θ)+μ(1−cos⁡θ)]y=−12A[(1−cos⁡θ)+μ(θ+sin⁡θ)]\begin{cases} &x=\frac{1}{2}A [(\theta-\sin\theta)+\mu(1-\cos\theta)] \newline &y=-\frac{1}{2}A [(1-\cos\theta)+\mu(\theta+\sin\theta)] \end{cases}

를 얻습니다. 마찰력 μ\mu의 값에 따른 곡선의 모양은 다음과 같습니다.

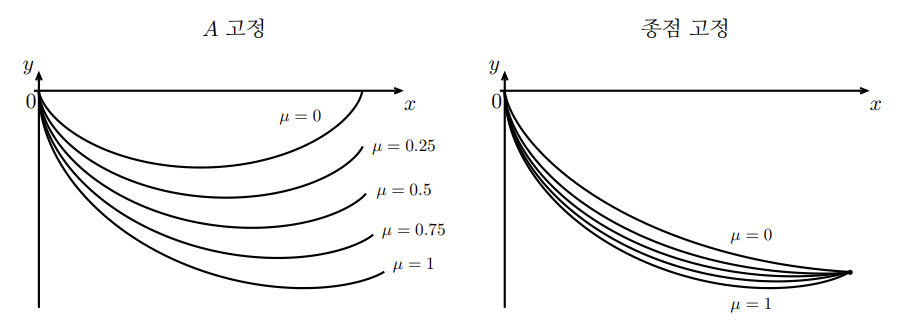마찰력 μ의 값에 따른 곡선의 모양마찰력 μ의 값에 따른 곡선의 모양

한 가지 흥미로운 점은 곡선을 어떻게 긋더라도 물체는 절대로 y+μx>0y+\mu x>0 인 곳으로 갈 수 없다는 것입니다. 일단 원점에서 곡선의 기울기가 −μ-\mu 보다 크다면 (즉, 더 완만하다면) 물체는 정지마찰력에 의해 움직이지 않습니다. 따라서 물체가 일단 움직이려면 y+μx<0y+\mu x<0 인 영역으로 움직여야 합니다. 그런데 아까 얻은 식 gy+μgx+12v2=0gy+\mu gx+\frac{1}{2}v^2=0 에 의하면 v2>0v^2>0이므로 항상 y+μx<0y+\mu x<0 입니다. 다시 말해 물체는 직선 y+μx=0y+\mu x=0 에 닿을수는 있어도 절대로 넘어갈 수 없다는 것입니다.

14장 (다중적분) 1번

지구 표면의 각 지점이 연간 받는 일조량을 구하는 식을 만들고, 이로부터 사막이 가장 많은 곳의 위도를 예측하라.

이 문제도 수식이 없는 문제입니다. 따라서 상황 해석부터 설정까지 전부 제가 해야 합니다. (개인적으로 이런 문제가 재밌는 것 같습니다.)

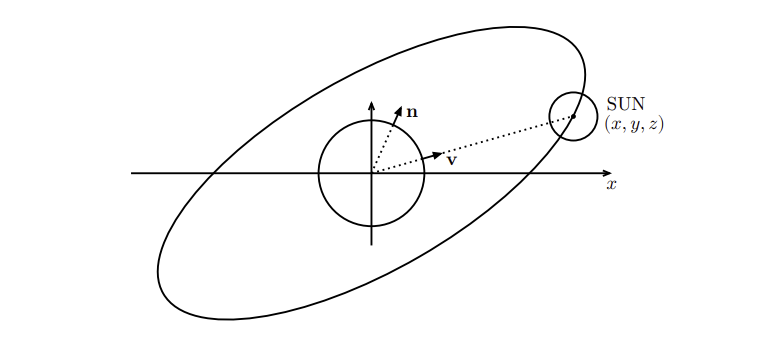상황 분석상황 분석

위 그림처럼 천동설로 생각해도 무방합니다. 또한 지구는 자전축이 기울어져 있습니다. 계산을 간단하게 하기 위해 지구는 그대로 두고 태양의 궤도를 자전축 기울기 ϕ\phi만큼 xx축 기준으로 회전합시다. 지구 반지름은 11, 태양의 궤도 반지름은 RR로 두었습니다.

지구 위의 점 (φ,θ)(\varphi, \theta)에서 법벡터는 n=(sin⁡φcos⁡θ,sin⁡φsin⁡θ,cos⁡φ)\mathbf{n}=(\sin\varphi \cos\theta, \sin\varphi \sin\theta, \cos\varphi)입니다. 태양이 공전 궤도 상에서 움직인 각도를 ξ\xi라고 하면 궤도를 xx축 기준으로 회전시키기 전의 좌표는 R(cos⁡ξ,sin⁡ξ,0)R(\cos\xi,\sin\xi,0)입니다. 따라서 회전시킨 후에는 R(cos⁡ξ,sin⁡ξcos⁡ϕ,sin⁡ξsin⁡ϕ)R(\cos\xi,\sin\xi \cos\phi, \sin\xi \sin\phi) 이 되고, 크기로 나눠주면 v=(cos⁡ξ,sin⁡ξcos⁡ϕ,sin⁡ξsin⁡ϕ)\mathbf{v}=(\cos\xi,\sin\xi \cos\phi, \sin\xi \sin\phi)를 얻습니다.

이제 지구상의 한 지점에서 빛의 세기 II는 법벡터와 태양각 사이의 각도 θ\theta에 대해 cos⁡θ\cos\theta에 비례하므로

I={n⋅v,n⋅v≥00,n⋅v<0I= \begin{cases} \mathbf{n}\cdot\mathbf{v}, &\mathbf{n}\cdot\mathbf{v} \geq 0 \newline 0, &\mathbf{n}\cdot\mathbf{v}<0 \end{cases}

라고 할 수 있습니다. 하루동안의 일조량 Id(ξ,φ)I_d (\xi,\varphi) 는

Id(ξ,φ)=∫02πmax⁡{I(θ,ξ,φ),0}dθI_d (\xi,\varphi) = \int_{0}^{2\pi} \max\{I(\theta,\xi,\varphi),0\} d \theta

이고, 일년 동안의 일조량 Iy(φ)I_y(\varphi)는

Iy(φ)=∫02πId(ξ,φ)dξI_y (\varphi) = \int_{0}^{2\pi} I_d (\xi,\varphi) d \xi

입니다. 따라서 Iy(φ)I_y (\varphi)가 최대가 되는 0≤φ≤π0 \leq \varphi \leq \pi를 찾으면 됩니다.

그런데 문제는.. 일단 Id(ξ,φ)I_d (\xi,\varphi)를 구하는 것 부터가 만만치 않습니다. Id(ξ,φ)I_d (\xi,\varphi)를 계산하기 위해서는 I(θ,ξ,φ)I(\theta,\xi,\varphi)가 양수가 되는 θ\theta의 범위를 구해야 하는데, 항이 3개나 있어서 범위를 정확히 구하는 것은 불가능 합니다. 설상가상으로 제가 애용하는 사이트인 desmos.com에서도 적분을 총 두번 하는 식을 입력하자 더 이상 작동하지 않고 고장이 나버렸습니다. 저는 위의 식을 계산할 수 있는 새로운 수학 소프트웨어를 찾아야만 했습니다.

그렇게 저는 처음으로 MATLAB을 사용해보게 되었습니다. 사전지식이 없는 상태였는데도 사용하는데 전혀 문제가 없었는데, 그냥 chatGPT한테 물어보니까 알아서 코드를 다 작성해 주더군요. 요즘 시대가 정말 좋아졌다는 것을 다시 한번 느끼는 순간이었습니다. MATLAB 코드는 아래와 같습니다.

% Main script
 
clear;  % 기존 변수를 제거하여 충돌을 방지
 
phi = 23.44*pi/180;  % phi 값 정의
 
% I 함수 정의
I = @(theta, ksi, varphi) (sin(varphi) .* cos(theta) .* cos(ksi)) + ...
                          (sin(varphi) .* sin(theta) .* sin(ksi) .* cos(phi)) + ...
                          (cos(varphi) .* sin(ksi) .* sin(phi));
 
% I_d 함수 정의
I_d = @(ksi, varphi) integral(@(theta) max(I(theta, ksi, varphi), 0), 0, 2*pi, 'ArrayValued', true);
 
% I_y 함수 정의
I_y = @(varphi) integral(@(ksi) I_d(ksi, varphi), 0, 2*pi, 'ArrayValued', true);
 
% I_y 그래프 그리기
varphi_values = linspace(0, pi, 100);
I_y_values = arrayfun(I_y, varphi_values);
 
figure;
plot(varphi_values, I_y_values);
 
title('I_y(\varphi) 그래프, phi=23.44deg');
xlabel('\varphi');
ylabel('I_y(\varphi)');

이 코드를 통해 다음의 그래프를 얻을 수 있습니다.

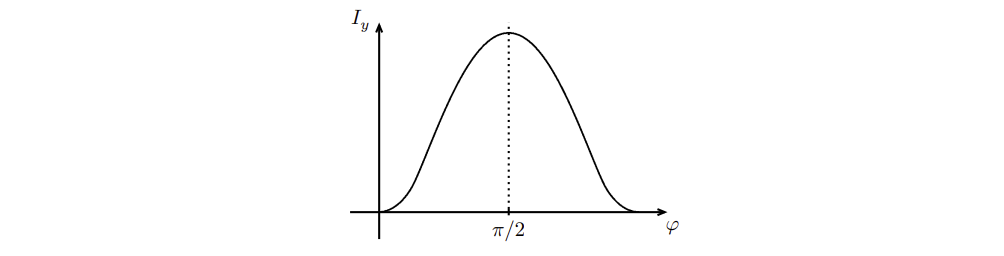위도에 따른 일조량 그래프위도에 따른 일조량 그래프

따라서 φ=π/2\varphi=\pi/2일 때, 즉 적도에서 가장 일조량이 큽니다. 개인적으로는 위도가 00이 아닌 곳이 나오기를 기대했는데 좀 아쉬웠습니다. 한 가지 흥미로운 점이 있다면, 지구의 자전축 기울기 ϕ\phi 값이 커짐에 따라 '적도'가 아닌 '극'(남극, 북극)에서의 일조량이 점점 커집니다. 대략 ϕ=0.94066684 rad\phi=0.94066684 \, \mathrm{rad}를 기점으로 일조량의 최댓값이 적도에서 극으로 옮겨가는데, 이 값을 닫힌 꼴로 구할 수 있을지 궁금합니다.

소감

탐구문제 풀이 기간은 12/18~12/20, 12/29~1/9로 대략 2주 정도 걸렸습니다. 이번에는 특히 typst나 MATLAB 등 수학과 관련된 다양한 도구들에 익숙해질 수 있었던 매우 유익한 시간이었습니다. 아직 다변수 미적분학이나 미분기하학 등 학문적으로는 이해하지 못한 부분들도 많지만, 분명 이러한 문제 풀이 경험은 나중에 공부를 하는데 큰 도움이 될 것이라고 생각합니다.

2024년에도 위상수학, 복소해석학, 푸리에 해석학 등 다양한 분야에서 학문적 발전을 이룰 수 있도록 노력하겠습니다.