김홍종 미적분학 1 탐구문제 풀이집 제작기

개요

서울대학교에서는 1학년에 수학 (또는 고급수학) 강의를 듣습니다. 교재는 김홍종 미적분학 1을 사용하는데 해당 교재는 오피셜 답지가 없기 때문에 문제를 풀더라도 답을 확인할 수 없습니다. 다행히 서울대 수리과학부의 하승우라는 분께서 만드신 미적분학 풀이집이 있어, 학생들은 공부를 할 때 해당 풀이집을 참고하여 공부합니다.

이 풀이집을 보면서 저도 뭔가 서울대학교에 이름을 남기고 싶다는 생각을 하던 와중, 탐구문제에는 아직 풀이집이 없다는 것을 알게 되었습니다. 탐구문제는 각 장의 마지막에 수록되어있는, 다소 오랜 시간동안 생각해야 하는 심화된 문제들입니다. 마침 제 수학 실력에 자부심도 가지고 있었기에 탐구문제 풀이집을 만들어 올려 보았습니다.

제작

풀이집 구성

김홍종 미적분학 1의 탐구문제는 총 9장으로 이루어져 있습니다. 관리를 쉽게 하기 위해서 아래처럼 각 장마다 하나의 파일을 만들어 풀이를 작성하였습니다.

장별로 파일 분리

각각의 문제에서는 풀이와 함께 해당 문제에서 생각할 수 있는 재미있는 사실이나, 따름 정리 등 빨간색 글씨로 밑에 적었습니다. 제가 평소에 jjycjn 같은 수학 블로그를 보는 것을 좋아하기 때문에 잡다한 정리들을 좀 많이 알고 있습니다. 수학을 좋아하는 사람이라면 빨간색 글씨를 재밌게 읽을 수 있을 것이라고 생각합니다.

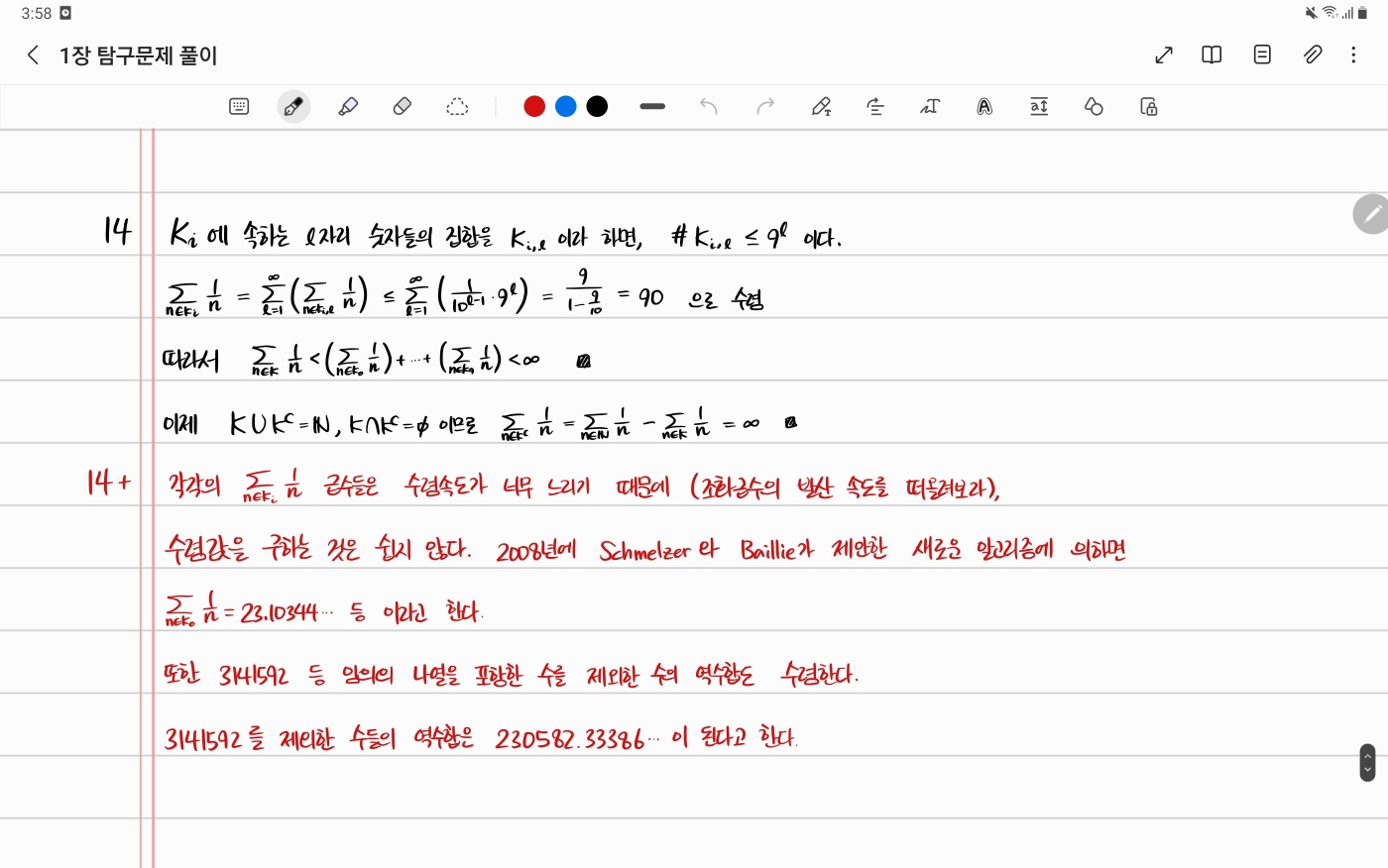빨간색 글씨로 추가적인 사실 정리

풀이집 다운로드 페이지

만들어진 풀이집 파일은 Dropbox 서비스를 통해 업로드 하였습니다. 그리고 노션을 사용하여 풀이집을 다운로드 할 수 있는 웹페이지를 만들었습니다. FAQ도 작성하여 왜 풀이집을 만들었는지, 혼자만의 힘으로 다 풀었는지, 오류를 제보하면 왜 상품을 주는지 등에 대한 질문을 적었습니다.

풀이집 다운로드 사이트

김홍종 미적분학 (3판) 탐구문제 풀이집

관심이 있으시다면 위 링크에 들어가셔서 한번 구경해보시기 바랍니다.

흥미로웠던 문제

전체 탐구문제 중에서 재미있었던 문제를 몇 개 소개해볼까 합니다.

3장 (테일러 전개) 13번

원점 근방에서 정의된 무한급수 $f$에 대하여 수열

$$\begin{equation*} f_0 := f(0), \, f_1 := f(1), \, f_2 := f(2), \cdots \end{equation*}$$

을 대응시키는 사상을 생각하자. 이 때 이 사상은 전사임을 보여라.

문제를 보자마자 테일러 전개에서 배운 내용이 떠올랐습니다. 무한 급수 $f(x)=\sum_{n=0}^\infty \frac{f_n}{n!} \,x^n$ 은 수렴 반경 내에서
$f^{(n)}(0)=f_n$을 만족합니다. 즉 사상 $T : C^\infty (\mathbb{R}) \rarr {\mathbb{R}}^\omega$의 공역에서 뽑은 임의의 원소 $(f_n)_{\,n\ge0}$ 에 대하여

로 잡으면, $f(x)$는 무한급이고 $f^{(n)}(0)=f_n$이 만족되어 증명이 끝납니다.

그런데 여기까지 풀이를 적었을때, 문득 $f(x)$의 수렴 반경이 $R=0$ 이면 어떡하지? 라는 생각이 들었습니다.
예를 들어 $f_n = n^n$인 경우에 모든 $x \neq 0$에 대해 $f(x)$는 발산하고 따라서 $f^{(n)}(0)=f_n$ 인 함수의 존재성을 보일 수 없습니다. 따라서 명제 자체가 틀린 것이 아닐까 하는 의문까지 들었으며 결국에는 인터넷과 다른 사람의 도움을 받게 되었습니다.

해당 정리는 Borel's theorem으로서 모든 멱급수에 대해 어떤 매끄러운 함수가 존재하여 이 함수의 테일러 급수가 처음의 멱급수와 같다는 정리입니다. 증명의 아이디어는 아래와 같습니다.

우리는 임의의 무한 수열 $(c_n)_{\,n\ge0}$에 대해 원점에서의 테일러 급수가 $\sum_{n=0}^{\infty} c_n x^n$ 인 함수를 찾고자 합니다. 위에서도 언급했듯이 가장 쉽게 떠올릴 수 있는 함수는

이지만, 해당 함수가 원점 근방에서 수렴함이 보장되지 않는다면 증명에 이용할 수 없습니다.

이제 smooth bump function $\psi$를 잡는데, $\psi(x)=1\enspace (|x|\le1),\enspace \psi(x)=0\enspace (|x|\ge2)$ 를 만족하도록 합니다. smooth function 이라 함은 모든 점에서 무한번 미분 가능한 함수를 뜻하고 bump function 이라는 이름은 $\psi$ 함수의 모양이 가운데가 볼록 튀어나와 있다는 것을 의미합니다. 이제 새로운 함수 $f(x)$를

와 같이 잡습니다. 단, $H_n$은 아래를 만족하는 수열입니다. ($x^{\underline{k}}=x\sdot(x-1) \cdots(x-k+1)$)

식이 다소 괴랄하게 생기긴 했지만, 아이디어를 이해할 때에 모든 식을 정확히 이해할 필요는 없습니다. $|c_n|$이 커질수록 $H_n$도 증가하는 것에 집중합시다. $f(x)$의 계수 $c_n \psi( H_n x)$는 $x \ge \frac{2}{H_n}$ 에서 항등적으로 $0$입니다. 즉 $H_n$이 크다면 $|x|$가 조금만 증가해도 $c_n \psi( H_n x)$는 금방 $0$이 될 것입니다. 이렇게 $\psi( H_n x)$는 $x \neq 0$에서도 $f(x)$가 수렴하도록 해주는 역할이라고 보시면 됩니다. 그러나 $x=0$ 에서는 여전히 $c_n \psi( H_n x) = c_n$ 이므로, $f^{(k)}(0)=k!c_k$ 가 성립할 것이라고 예상할 수 있습니다. 따라서 증명 끝.

위의 아이디어를 바탕으로 한 더욱 엄밀한 증명은 nLab 에서 보실 수 있습니다.

7장 (정사각행렬과 행렬식) 24번

동서 방향과 남북방향으로 금이 쳐져 있는 한 없이 넓은 좌표평면 위에 주사위가 놓여 있다. 아래 그림의 왼쪽에 있는 주사위를 동서 방향 또는 남북 방향으로 여러번 굴려서 오른쪽 주사위의 상태로 옮기려면 어떻게 굴리면 될까? (한 번 굴릴 때에는 주사위의 한 모서리를 따라 90◦ 회전시킨다.)

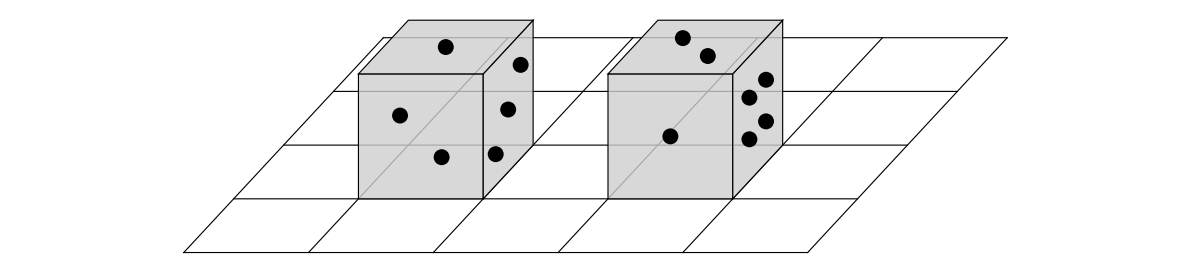탐구문제 7장 24번 그림

일단 주어진 문제 상황이 추상적이기 때문에 수학적으로 주사위를 정의해야합니다. 위치는 $2$차원 벡터인 $(x, y)$로 정의합니다. 지문의 왼쪽 주사위는 $(0,0)$, 오른쪽 주사위는 $(2,0)$ 입니다. 그리고 주사위의 상태를 $3$차원의 벡터인 $(u, r, f)$로 정의합니다. 단, $u, r, f$는 각각 주사위의 위(up), 오른쪽(right), 앞(front)의 숫자입니다. 예를 들어 지문의 왼쪽 주사위는 $S=(1,3,2)$ 입니다.

다음으로는 주사위의 굴림을 정의해보겠습니다. $x$ 방향(오른쪽)으로 한번 굴리면, 상태 $S=(u,r,f)$는 $S'=(7-r,u,f)$가 됩니다. 주사위의 숫자를 $1, 2, 3, 4, 5, 6$이 아닌 $1, 2, 3, -3, -2, -1$로 본다면 (즉, $\mathrm{mod}\,7$로 본다면) $x$ 방향의 굴림은 $(u,r,f) \mapsto (-r,u,f)$이므로 선형사상이 됩니다. 따라서

로 정의하면 $x$방향으로의 굴림을 잘 정의할 수 있습니다. 마찬가지로

로 정의하면 $-x, y, -y$ 방향으로의 굴림을 행렬을 사용해 정의할 수 있습니다. 당연하지만 $R_{-x}=R_x^{\;-1}, R_{-y}=R_y^{\;-1}$ 입니다.

이제 다시 문제로 돌아가서, 처음 상태 $S=(1,3,2)$ 에서 마지막 상태 $S'=(2,-3,1)$ 로 가기 위해서는 행렬

이 곱해져야 합니다. 따라서 우리의 목표는 행렬 $R_x, R_{-x}, R_y, R_{-y}$들의 곱으로 $R$을 표현하는 것입니다. 단, $R_x$의 개수에서 $R_{-x}$의 개수를 빼면 $2$가 나와야 하고, $R_y$의 개수와 $R_{-y}$의 개수는 같아야 합니다. 그래야 최종적으로 위치 $(2,0)$에 주사위가 멈출 수 있습니다. 여기서부터는 sagemath를 사용해 재귀호출로 해가 존재하는지 찾아보았습니다.

R_x = Matrix([[0,-1,0],[1,0,0],[0,0,1]])
R_invx = Matrix([[0,1,0],[-1,0,0],[0,0,1]])
R_y = Matrix([[0,0,1],[0,1,0],[-1,0,0]])
R_invy = Matrix([[0,0,-1],[0,1,0],[1,0,0]])
 
target = Matrix([[0,0,1],[0,-1,0],[1,0,0]])
 
matrices = [R_x, R_invx, R_y, R_invy]
deltaX = [1, -1, 0, 0]
deltaY = [0, 0, 1, -1]
 
n = 14 #재귀호출의 깊이
 
matrix_by_level = [0] * n
 
def f(level, x, y):
    if level >= n:
        if x == 2 and y == 0:
            product = identity_matrix(3)
            for i in range(n):
                product *= matrix_by_level[i]
            if (product - target).is_zero():
                print(matrix_by_level)
    else:
        for i in range(4):
            matrix_by_level[level] = matrices[i]
            f(level+1, x + deltaX[i], y + deltaY[i])
 
f(0, 0, 0)

그러나 재귀호출의 깊이를 $n=2$ 부터 $n=14$ 까지 늘려봤는데도 해는 하나도 존재하지 않았습니다. 뭔가 코딩이 잘못되었나 하면서, 최종 주사위의 위치가 $(2,0)$이라는 조건 x == 2 and y == 0을 없앤 뒤에 다시 재귀호출을 돌려보았습니다. 그리고 해가 존재할 경우 (x, y)를 출력하도록 하였습니다. 그 위치들을 좌표 평면에 나타내었더니 신기한 결과가 나왔습니다.

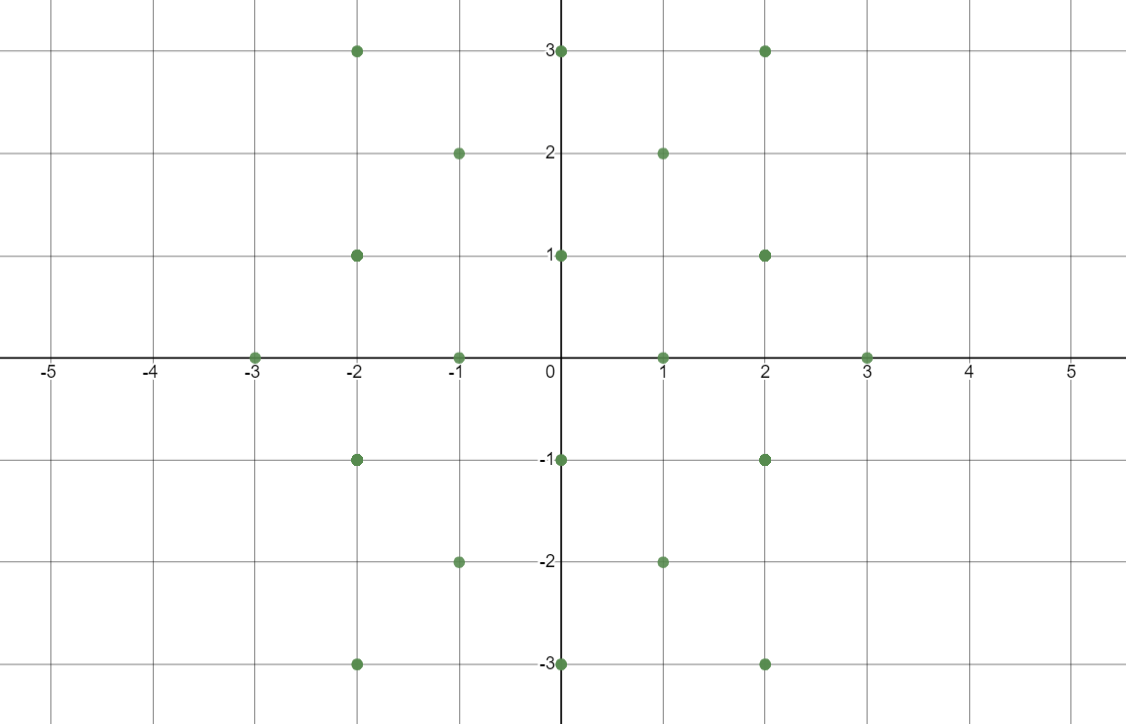n=5일 때 주사위의 위치

위 그래프는 $n=5$일 때 최종 상태가 $S=(2,-3,1)$인 주사위들의 위치입니다. 한 칸씩 떨어지면서 일정한 패턴을 이루는 모습을 볼 수 있습니다. (엄밀하게 말하자면, 이 점들은 모두 $x+y$의 홀짝성이 같은 점들입니다.) 우리의 목표는 최종 상태가 $S=(2,-3,1)$ 이면서 위치가 $(2,0)$에 있는 주사위를 찾는 것이므로, 해당 주사위는 존재하지 않겠다는 강력한 심증을 가지게 해줍니다.

답이 존재하지 않는다임을 알게 되면, 수학에서는 굉장히 자주 쓰는 방법이 있습니다. 바로 불변량을 찾는 것입니다.

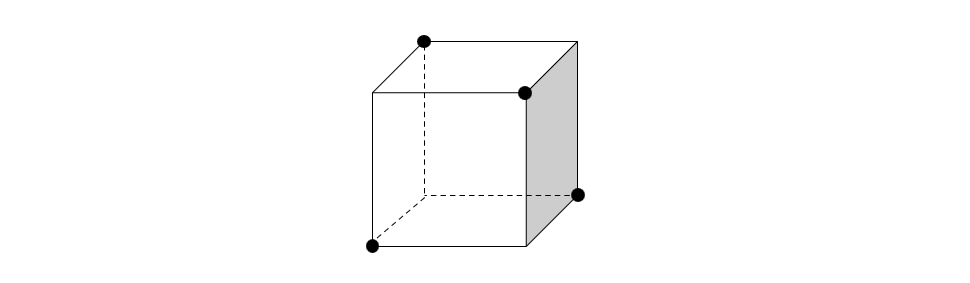주사위의 불변량

주사위에서 $1, 2, 3$이 적힌 면이 만나는 점의 위치에 따라 주사위의 특성 $C$를 정의합니다. 위 그림의 검은색 점 위치에 있을 경우 $C=0$, 그렇지 않을 경우 $C=1$로 정의합니다. 이 때 어떤 주사위를 굴려 얻은 모든 주사위에 대해서 $C+x+y$의 홀짝성은 같습니다. 증명은 간단한데, 주사위를 한번 굴리면 $C$도 $1$만큼 변하고 $x+y$도 $1$만큼 변해서 결국 $C+x+y$의 홀짝성은 일정하기 때문입니다. 이제 지문의 왼쪽 주사위는 $C+x+y=1+0+0=1$, 오른쪽 주사위는 $C+x+y=0+2+0=2$ 으로 홀짝성이 달라 불가능합니다. 증명 끝.

사실 방금의 증명은 저희가 위에서 발견한 신기한 명제, 상태가 $S$인 주사위를 굴려 상태가 $S'$인 주사위를 얻고자 할 때 $x+y$의 홀짝성이 같은 점들에서 가능하다는 명제를 포함하고 있지는 않습니다. 이 사실을 조금 더 깔끔하게 쓰면 아래와 같습니다.

위치 $P=(x,y)$, 상태 $S=(u,r,f)$를 가지는 주사위를 $D=(P,G)$ 라고 하자.
그리고 $\mathrm{sum}P := x+y$로 정의하자.
$D$를 굴려 얻은 주사위 중에서 $D'=(P',S)$가 존재한다는 것은 $\mathrm{sum}P \equiv \mathrm{sum}P' \;\;(\mathrm{mod}2)$와 동치이다.

소감

탐구문제 풀이 작성은 6월 13일에 시작해서 7월 1일에 마쳤는데, 중간에 여행갔던 것을 제외하면 2주 정도 소요되었습니다. 중간에 어렵고 귀찮은 문제들도 많아서 힘들었는데 이렇게 답지를 완성하고 나니 매우 뿌듯합니다. 미적분학 1 교재를 마스터 했다고 할 수 있을 정도로 개념을 완벽하게 이해하게 된 것 같습니다.

2학기에도 열심히 공부하여서 미적분학 2 탐구문제 풀이집을 만들 수 있는 실력을 갖추도록 노력해보겠습니다.