퀵 정렬의 원리와 성능 향상을 위한 최적화 기법
이미 정렬되어 있는 경우, 비슷한 원소가 많은 경우 알고리즘을 수정해보자
2024-11-10
-
개요
퀵 정렬은 분할 정복을 이용하는 알고리즘 중 하나입니다. 기준 원소를 하나 잡아 기준 원소보다 작은 원소와 큰 원소 그룹으로 나눈 뒤, 각각을 정렬하는 방법입니다. 평균적으로 의 시간복잡도를 가지며, 매우 좋은 성능을 보입니다.
그러나 정렬할 데이터의 특성에 따라 최악의 경우에는 의 시간복잡도를 가지기도 합니다. 이 글에서는 먼저 퀵 정렬의 작동 방식을 살펴보고, 그 이후에 퀵 정렬이 느려지는 경우들과 각각의 해결 방법에 대해서 알아보도록 하겠습니다.
퀵 정렬 알고리즘
 퀵 정렬 핵심 알고리즘
퀵 정렬 핵심 알고리즘
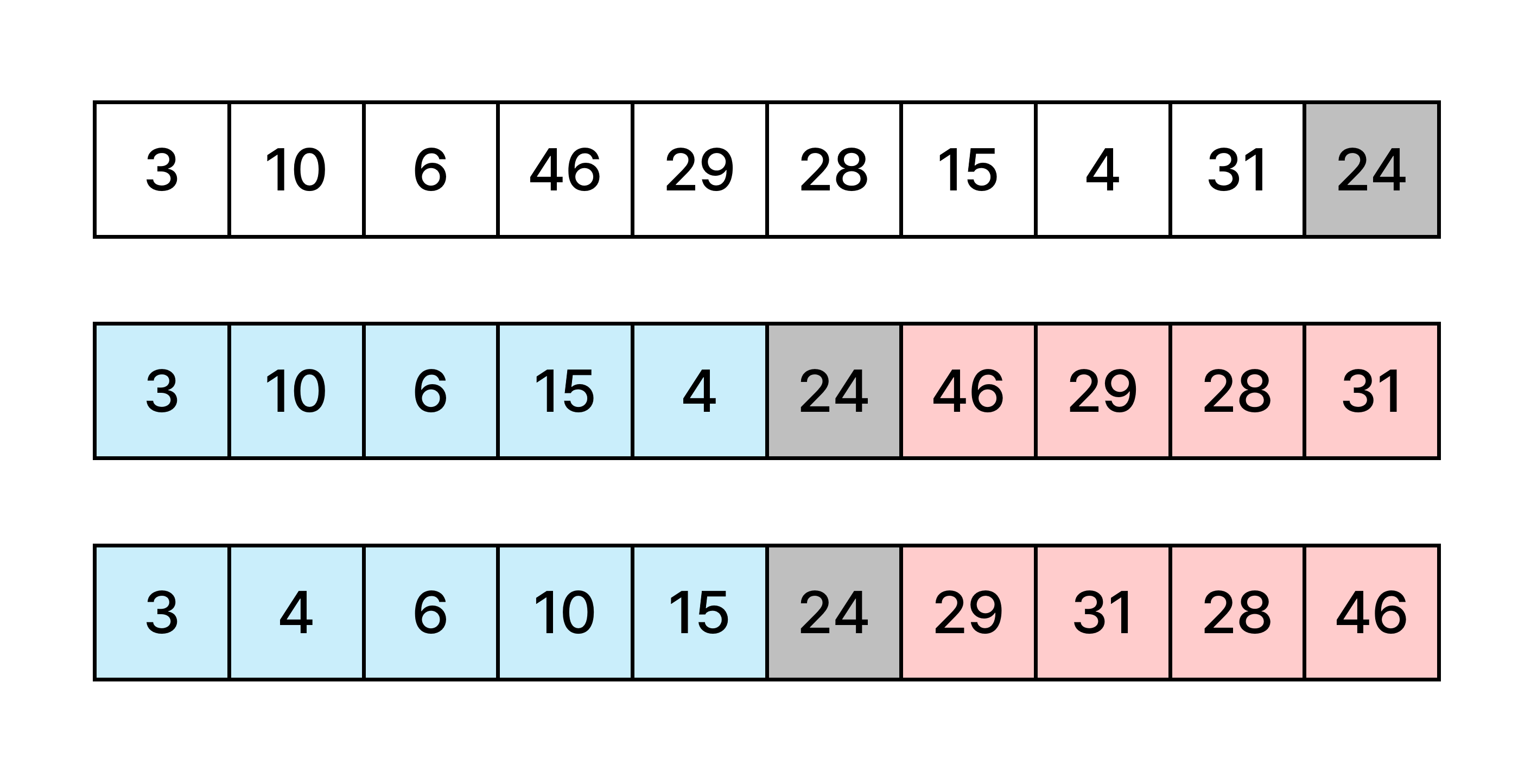
위는 퀵 정렬의 핵심 알고리즘을 나타낸 사진입니다.
- 첫 번째 줄에 정렬할 배열이 주어졌습니다.
- 이제 기준 원소를 잡아 기준 원소보다 작은 숫자는 앞쪽에, 큰 숫자는 뒷쪽에 재배치합니다. (기준 원소는 아무렇게나 잡아도 상관 없지만, 여기서는 맨 뒤의 원소로 잡았습니다.)
- 그 다음으로 기준 원소의 앞쪽 그룹과 뒷쪽 그룹을 각각 정렬합니다.
이 때 앞쪽 그룹이나 뒷쪽 그룹이 정렬되더라도 기준 원소의 자리는 영향을 받지 않습니다. 즉 기준 원소는 앞쪽, 뒷쪽 그룹의 정렬을 시작하기도 전에 이미 제자리를 찾은 것입니다. 따라서 앞쪽 그룹과 뒷쪽 그룹의 정렬이 끝나는 순간 전체 배열의 정렬이 완료됩니다. 앞쪽, 뒷쪽 그룹의 정렬에는 퀵 정렬을 재귀적으로 사용하면 됩니다.
퀵 정렬 알고리즘을 유사코드로 나타내면 아래와 같습니다. 최초의 호출은 quickSort(A, 0, n-1) 입니다.
quickSort(A[], p, r):
if p < r
q <- partition(A, p, r)
quickSort(A, p, q-1)
quickSort(A, q, r)
partition(A[], p, r):
배열 A[p...r]의 원소들을 기준 원소인 A[r]과의 상대적 크기에 따라
양쪽으로 재배치하고, 기준 원소가 자리한 위치를 반환한다기준 원소를 중심으로 분할하는 방법에는 여러 가지가 있습니다. 특별히 비효율적이지 않다면 어떤 방법을 사용해도 문제는 없습니다. 대표적인 분할 방법은 다음과 같습니다.
partition(A[], p, r):
x <- A[r]
i <- p-1
for j <- p to r-1
if A[j] < x
A[++i] <-> A[j]
A[i+1] <-> A[r]
return i+1예시를 통해서 위의 알고리즘을 이해해보겠습니다. 목표는 기준 원소보다 작은 원소는 왼쪽에, 기준 원소보다 크거나 같은 원소는 오른쪽에 오도록 원소들을 재배치하는 것입니다. 알고리즘은 원소들을 다음의 네 구역으로 나누어 관리합니다.
- 1구역: 기준 원소보다 작은 원소들 (파란색)
- 2구역: 기준 원소보다 크거나 같은 원소들 (빨간색)
- 3구역: 아직 정해지지 않은 원소들 (흰색)
- 4구역: 기준 원소 자신 (검은색)
 partition 중간의 한 단계
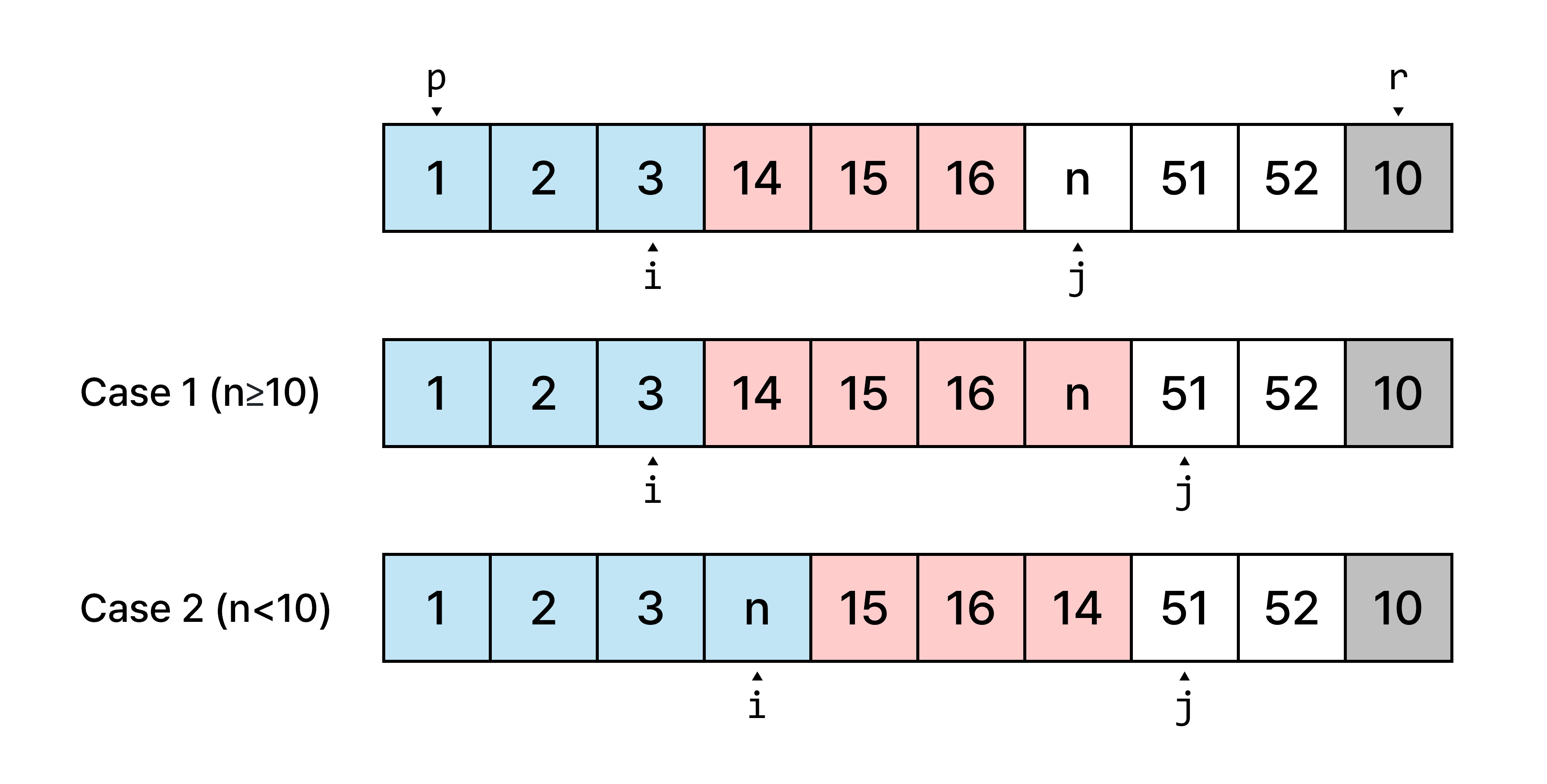
partition 중간의 한 단계
3구역에 있는 원소들을 차례로 하나씩 보면서 1구역 또는 2구역에 포함시킵니다. 변수 i는 1구역의 오른쪽 끝을 가리키고, 변수 j는 3구역의 왼쪽 끝을 가리킵니다. 2구역은 이 둘의 사이에 해당하므로 2구역을 표시하기 위해 새로운 변수를 만들 필요는 없습니다. 처음에는 어떤 원소도 보지 않았으므로 기준 원소를 제외한 모든 원소가 3구역에 속합니다. for 루프를 돌 때마다 원소를 하나씩 보기 때문에 j는 항상 1씩 증가합니다.
3구역의 첫 번째 원소가 기준 원소보다 크거나 같은 경우에는 2구역에 포함시켜야 하므로 2구역이 한 칸 넓어져야 합니다. 이 경우에는 따로 해줄 일이 없습니다. for 루프가 한 번 돌았으므로 j는 자동으로 1 증가합니다. i은 바뀌지 않고 j만 증가하므로 2구역이 한 칸 넓어집니다. 위 사진에서 case 1에 해당하는 경우입니다.
3구역의 첫 번째 원소가 기준 원소보다 작은 경우에는 1구역에 포함시켜야 합니다. i값을 1 증가시킨 다음 2구역의 첫 번째 원소 A[i]와 3구역의 첫 번째 원소 A[j]를 교환합니다. 루프가 끝나면 j값도 1 증가하게 되고, 결론적으로 1구역만 한 칸 넓어집니다. 위 사진에서 case 2에 해당하는 경우입니다.
3구역을 모두 소진하고 나면 마지막 처리만 남습니다. 2구역의 첫 번째 원소와 기준 원소의 자리를 바꾸는 것입니다. 그러면 기준 원소 기준으로 왼쪽에는 작은 값들이, 오른쪽에는 크거나 같은 값들이 존재하게 됩니다. 이제 기준 원소의 위치인 i+1을 리턴하면 끝납니다.
시간복잡도
 퀵 정렬의 진행 과정
퀵 정렬의 진행 과정
퀵 정렬은 평균적으로 의 시간복잡도를 가집니다. 조금 더 정확히 말하자면, 평균 의 시간복잡도를 가집니다. 왜냐하면 각 단계에서 정렬해야 하는 배열의 크기가 절반씩 줄어들기 때문입니다. 정렬해야 하는 배열의 크기가 일 때 걸리는 시간을 이라고 하면, 왼쪽 그룹과 뒷쪽 그룹을 정렬하는데 각각 의 시간이 걸리고, partition 알고리즘을 수행하는데 의 시간이 걸리므로 점화식은 다음과 같습니다.
이 점화식을 풀면 을 얻게 됩니다.
big-O 기호는 해당 함수보다 차수가 작거나 같은 함수들을 뜻합니다.
반면, big-Theta 기호는 해당 함수와 차수가 정확히 같은 함수들을 뜻합니다.
퀵 정렬이 O(n^2)으로 느려지는 경우
최악의 경우는 분할 시에 한쪽 그룹은 거의 없고 다른 쪽에 다 몰리도록 분할되는 일이 반복되는 경우입니다. 그러면 길이 의 배열을 정렬할 때 한 쪽 그룹을 정렬하는데 의 시간이 걸리고, partition 알고리즘을 수행하는데 의 시간이 걸리므로 위의 점화식이 아래와 같이 바뀌게 됩니다.
결국 전체 배열을 정렬하는데 의 시간이 걸리게 됩니다. 이렇게 균형이 맞지 않는 원인에는 크게 두 가지가 있습니다.
이미 정렬되어 있는 경우
 이미 정렬되어 있는 경우
이미 정렬되어 있는 경우
첫 번째는 배열이 이미 정렬되어 있거나 거의 정렬되어 있는 경우입니다. 역순으로 정렬되어 있을 때도 마찬가지입니다. 이 경우에는 분할시 모든 원소가 한 쪽 그룹에 몰리게 됩니다. 결국 배열의 크기는 한 칸씩 밖에 줄어들지 않아 에 비례하는 시간이 걸리게 됩니다.
동일한 원소가 많은 경우
 배열에 1, 2, 3만 있는 경우
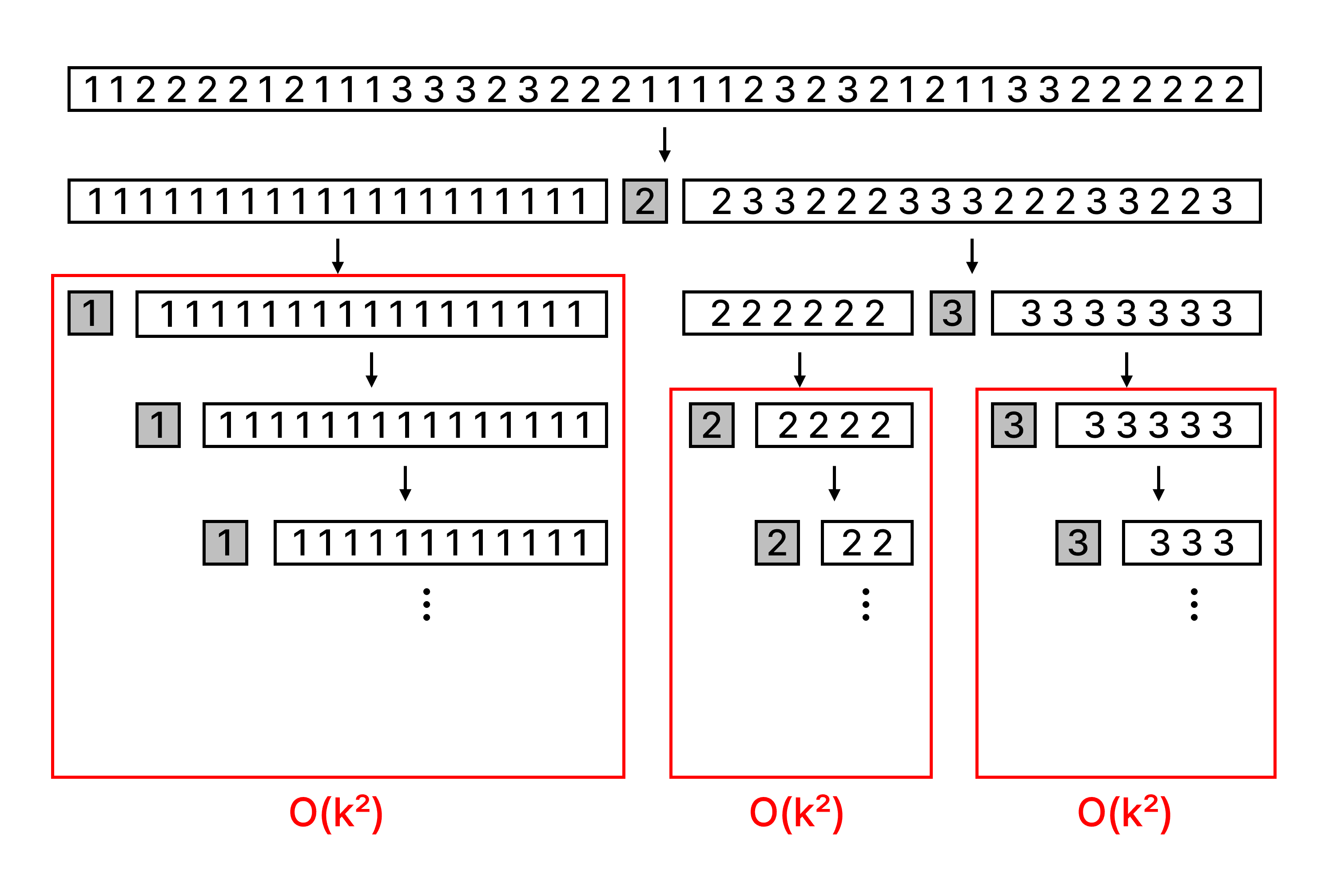
배열에 1, 2, 3만 있는 경우
두 번째는 배열에 동일한 원소가 많이 존재하는 경우입니다. 입력의 모든 원소가 동일한 극단적인 경우라면 이미 정렬되어 있는 경우처럼 분할이 최악이 됩니다. 모든 원소가 동일하지는 않더라도 중복이 충분히 많다면 그에 비례해서 성능이 떨어집니다. 퀵 정렬을 진행하다 보면 같은 원소들은 한 덩어리로 모이는데, 이 때 크기가 인 덩어리는 로 분할됩니다. 결국 이 덩어리는 정렬하는데 의 시간이 걸리게 됩니다. 이러한 덩어리들이 많다면 전체 배열의 정렬 시간에서도 무시하지 못할 정도가 되며, 총 정렬 시간이 에 맞먹게 됩니다.
알고리즘 수정
이제 배열이 이미 정렬된 경우와 비슷한 원소가 많은 경우 각각에서 알고리즘이 느려지지 않도록 어떻게 수정할 수 있을지 알아보겠습니다.
이미 정렬되어 있는 경우
배열이 정렬된 경우에는 다음의 두 가지 방법이 있습니다.
1. 기준 원소를 무작위로 정하기 (Randomized Quick Sort)
partition(A[], p, r):
pivot <- random_int(p,r)
A[pivot] <-> A[r]
x <- A[r]
i <- p-1
for j <- p to r-1
if A[j] < x
A[++i] <-> A[j]
A[i+1] <-> A[r]
return i+1기준이 되는 원소를 임의의 위치에서 뽑는 방법입니다. 이미 정렬된 배열이라도 피벗이 특정 방향으로 치우치지 않아 분할시 쏠림이 줄어듭니다.
2. 중위 값을 기준 원소로 정하기 (Median of Three Quick Sort)
partition(A[], p, r):
mid <- (p+r)/2
pivot <- median(p, mid, r) // A[p], A[mid], A[r] 중 중위값을 가지는 인덱스
A[pivot] <-> A[r]
x <- A[r]
i <- p-1
for j <- p to r-1
if A[j] < x
A[++i] <-> A[j]
A[i+1] <-> A[r]
return i+1배열의 왼쪽 끝, 가운데, 오른쪽 끝 원소중 중위값을 기준 원소로 두는 방법입니다. 이전 방법과 마찬가지로 분할이 한 쪽으로 쏠리지 않도록 해줍니다.
성능 테스트
 정렬된 비율에 따른 정렬 시간 (n = 1000)
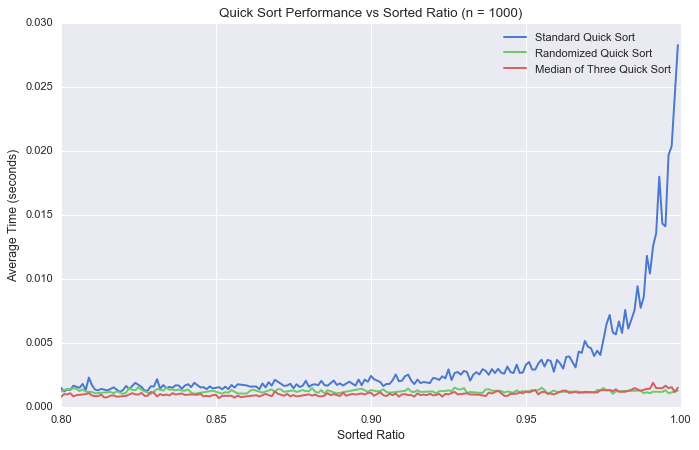
정렬된 비율에 따른 정렬 시간 (n = 1000)
원소의 개수가 1000개인 경우 정렬된 비율에 따른 정렬 시간을 계산해보았습니다. 정렬된 비율이 1에 가까워질수록 기존 퀵 정렬 알고리즘의 시간은 점점 증가하는 반면, 수정된 알고리즘은 동일한 성능을 보여주고 있습니다.
참고로 정렬된 비율 sorted_ratio이 주어졌을 때, 무작위로 생성된 배열에서 n*sorted_ratio개의 index를 무작위로 뽑아 해당 index의 원소들끼리 정렬을 하여 배열을 생성하였습니다.
비슷한 원소가 많은 경우
비슷한 원소가 많은 경우에도 두 가지 알고리즘을 소개하겠습니다.
1. 기준 원소와 같으면 무작위 방향으로 옮기기 (Randomized Equal Element Quick Sort)
partition(A[], p, r):
x <- A[r]
i <- p-1
for j <- p to r-1
if A[j] < x or (A[j] = x and random(0,1) > 1/2)
A[++i] <-> A[j]
A[i+1] <-> A[r]
return i+1기준 원소와 같은 원소를 왼쪽 또는 오른쪽으로 랜덤하게 이동시키는 방법입니다. 확률상 반반으로 분리되므로, 분할이 한 쪽으로 쏠리지 않습니다.
2. 원소를 세 구역으로 분할하기 (3-Way Quick Sort)
quickSort(A[], p, r):
if p < r
(q, t) <- partition(A, p, r)
quickSort(A, p, q-1)
quickSort(A, t+1, r)
partition(A[], p, r):
배열 A[p...r]의 원소들을 기준 원소인 A[r]과의 상대적 크기에 따라
세 구역(>, =, <)으로 재배치하고, 기준 원소와 같은 원소들의 구역의 왼쪽 끝과 오른쪽 끝 위치를 반환한다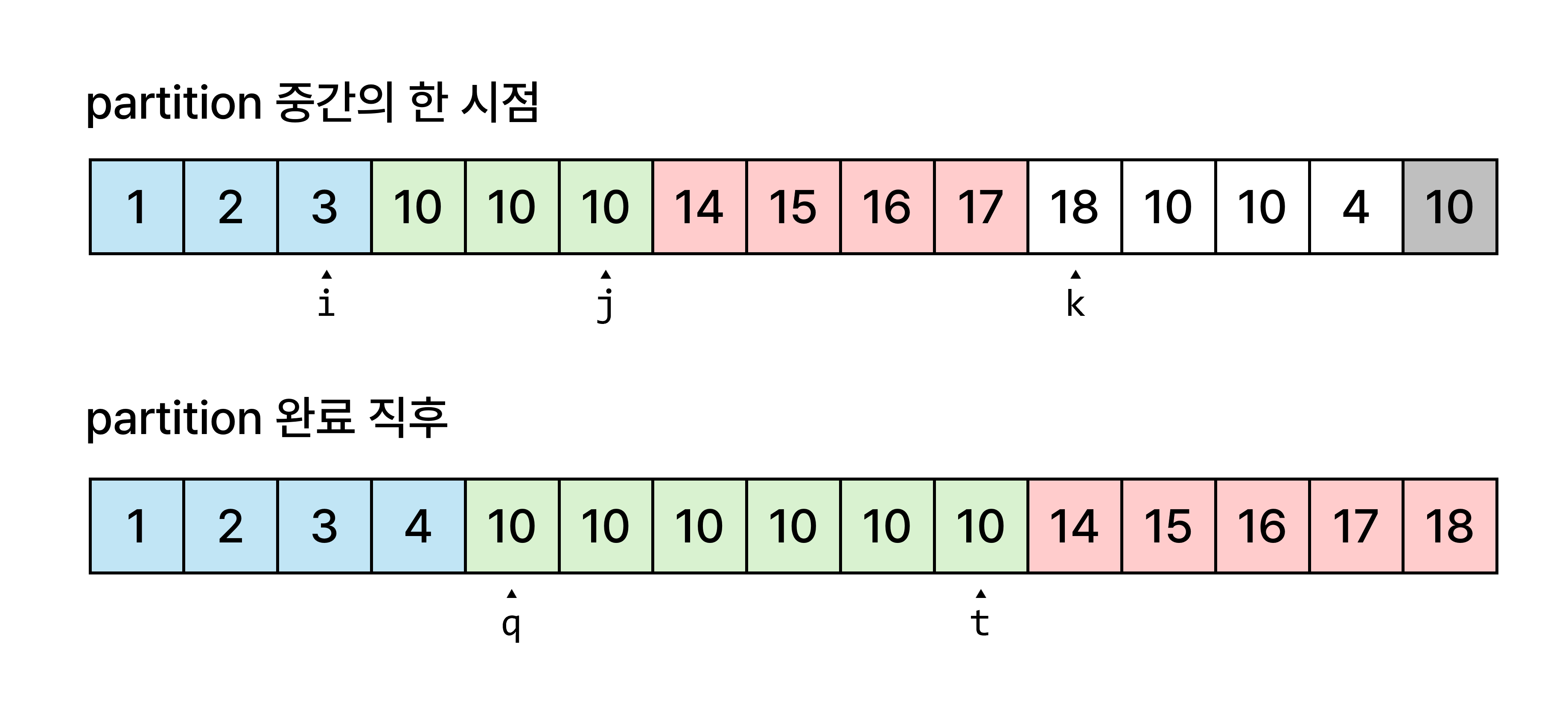 원소들을 세 구역으로 분할
원소들을 세 구역으로 분할
기준 원소보다 작은 그룹, 같은 그룹, 큰 그룹 총 세 구역으로 나누어 분할하는 방법입니다. 구현은 조금 더 복잡하지만 문제를 확실하게 해결할 수 있습니다.
partition 알고리즘은 특별히 느리지만 않다면 어떻게 구현해도 상관 없습니다. 아래는 한 구현 예시입니다.
partition(A[], p, r):
x <- A[r]
i <- p-1
j <- p-1
for k <- p to r-1
if A[k] < x
A[++i] <-> A[k]
A[++j] <-> A[k]
if A[k] = x
A[++j] <-> A[k]
A[j+1] <-> A[r]
return (i+1, j+1)
성능 테스트
 같은 원소의 개수에 따른 정렬 시간 (n = 1000)
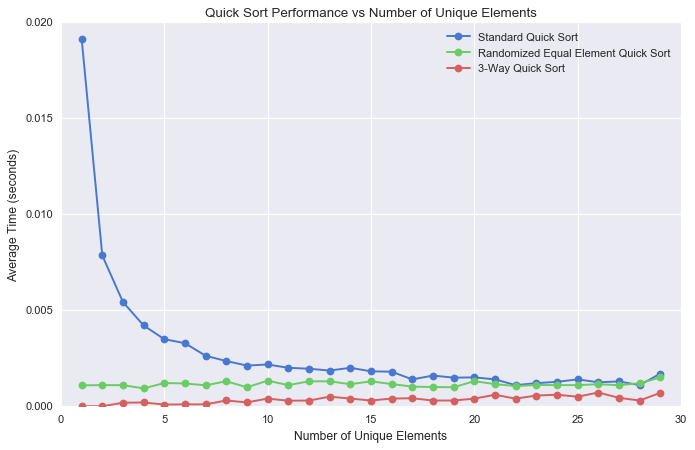
같은 원소의 개수에 따른 정렬 시간 (n = 1000)
원소의 개수가 1000개인 경우 같은 원소의 개수에 따른 정렬 시간을 계산해보았습니다. 동일한 원소의 개수가 적어질수록 기존 퀵 소트 정렬의 시간은 크게 증가하는 반면, 수정된 알고리즘은 동일한 성능을 보여주고 있습니다.
다만 평균적으로 Randomized Equal Element Quick Sort에 비해 3-Way Quick Sort가 더욱 짧은 시간만에 정렬을 완료하고 있습니다. 기준 원소와 동일한 원소가 있을 때 전자는 아무튼 둘 중 한 그룹에 포함시키는 반면 후자는 아예 배제를 하기 때문에 더 빠르다고 추측해볼 수 있습니다.
참고 자료
- 문병로.『쉽게 배우는 자료구조 with 자바』. 한빛아카데미, 2022.
© 2025 geniusLHS. All rights reserved.